


Next: The 1-d wave equation
Up: The wave equation
Previous: The Crank-Nicholson scheme
Upwind differencing
We might be forgiven for concluding that the Crank-Nicholson scheme represents an
efficient and accurate general purpose numerical method for solving the advection equation.
This is indeed the case, provided we restrict ourselves to fairly smooth wave-forms.
Unfortunately, the Crank-Nicholson scheme does a very poor
job at advecting wave-forms with sharp leading or trailing edges. This is illustrated in
Fig. 78, which shows a calculation in which the Crank-Nicholson scheme
is used to advect a square wave-pulse. It can be seen that spurious oscillations are generated
at both the leading and trailing edges of the wave-form. It turns out that all central
difference schemes for solving the advection equation suffer from a
similar problem.
Figure 78:
Advection of a 1-d square wave-pulse.
Numerical calculation performed using
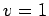 ,
,
 , and
, and 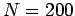 . The
dotted curve shows the initial condition at
. The
dotted curve shows the initial condition at 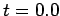 , whereas the solid curve shows the numerical solution
at
, whereas the solid curve shows the numerical solution
at 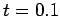 .
.
 |
The only known way to suppress spurious oscillations
at the leading and trailing edges of a sharp wave-form is to adopt a so-called upwind
differencing scheme. In such a scheme, the spatial differences are skewed in the ``upwind''
direction: i.e., the direction from which the advecting flow emanates. Thus, the
upwind version of the simple explicit differencing scheme (236)
is written
 |
(248) |
or
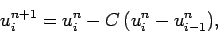 |
(249) |
Note that this scheme is only first-order in space, whereas every other scheme
we have discussed has been second-order. A von Neumann stability analysis
of the above scheme yields
![\begin{displaymath}
A = 1 - C\,[1-\cos (k \,\delta x)]-{\rm i} \,C\,\sin (k \,\delta x).
\end{displaymath}](img976.png) |
(250) |
Note that
![\begin{displaymath}
\vert A\vert^2 =1-2\,C\,(1-C)\,[1-\cos (k \,\delta x)].
\end{displaymath}](img977.png) |
(251) |
It follows that 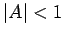 for all
for all 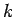 provided that
provided that 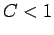 . Thus, the upwind differencing
scheme is stable provided that the CFL condition is satisfied.
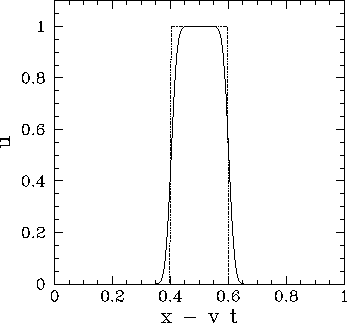
Fig. 79 shows a calculation in which the above scheme
is used to advect a square wave-pulse. There are now no spurious oscillations generated
at the sharp edges of the wave-form. On the other hand, the wave-form shows evidence
of dispersion. Indeed, the upwind differencing scheme suffers from the
same type of spurious dispersion problem as the Lax scheme.
Unfortunately, there is no known differencing scheme which is both
non-dispersive and
capable of dealing well with sharp wave-fronts.
In fact, sophisticated
codes which solve the advection (or wave) equation generally employ an upwind scheme in regions close to
sharp wave-fronts, or shocks, and a more accurate non-dispersive scheme elsewhere.
. Thus, the upwind differencing
scheme is stable provided that the CFL condition is satisfied.
Fig. 79 shows a calculation in which the above scheme
is used to advect a square wave-pulse. There are now no spurious oscillations generated
at the sharp edges of the wave-form. On the other hand, the wave-form shows evidence
of dispersion. Indeed, the upwind differencing scheme suffers from the
same type of spurious dispersion problem as the Lax scheme.
Unfortunately, there is no known differencing scheme which is both
non-dispersive and
capable of dealing well with sharp wave-fronts.
In fact, sophisticated
codes which solve the advection (or wave) equation generally employ an upwind scheme in regions close to
sharp wave-fronts, or shocks, and a more accurate non-dispersive scheme elsewhere.
Figure 79:
Advection of a 1-d square wave-pulse.
Numerical calculation performed using
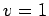 ,
,
 , and
, and 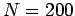 . The
dotted curve shows the initial condition at
. The
dotted curve shows the initial condition at 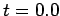 , whereas the solid curve shows the numerical solution
at
, whereas the solid curve shows the numerical solution
at 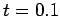 .
.
 |
Incidentally, it is easily demonstrated that the downwind differencing scheme,
 |
(252) |
is unconditionally unstable.



Next: The 1-d wave equation
Up: The wave equation
Previous: The Crank-Nicholson scheme
Richard Fitzpatrick
2006-03-29


