


Next: The Lax scheme
Up: The wave equation
Previous: Introduction
The wave equation is closely related to the so-called advection equation, which
in one dimension takes the form
 |
(234) |
This equation describes the passive advection of some scalar field 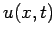 carried along by a flow of constant speed
carried along by a flow of constant speed 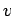 . Since the advection equation
is somewhat simpler than the wave equation, we shall discuss it first.
The advection equation
possesses the formal solution
. Since the advection equation
is somewhat simpler than the wave equation, we shall discuss it first.
The advection equation
possesses the formal solution
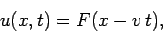 |
(235) |
where  is an arbitrary function. This solution describes an arbitrarily
shaped pulse which is swept along by the flow, at constant speed
is an arbitrary function. This solution describes an arbitrarily
shaped pulse which is swept along by the flow, at constant speed 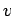 , without
changing shape.
, without
changing shape.
We seek the solution of Eq. (234) in the region
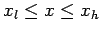 ,
subject to the simple Dirichlet boundary conditions
,
subject to the simple Dirichlet boundary conditions
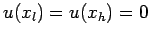 .
As usual, we discretize in time on the uniform grid
.
As usual, we discretize in time on the uniform grid
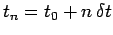 , for
, for
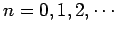 .
Furthermore, in the
.
Furthermore, in the  -direction, we discretize on the uniform grid
-direction, we discretize on the uniform grid
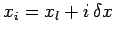 , for
, for
 , where
, where
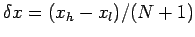 . Adopting an explicit temporal differencing
scheme, and a centered spatial differencing scheme, Eq. (234) yields
. Adopting an explicit temporal differencing
scheme, and a centered spatial differencing scheme, Eq. (234) yields
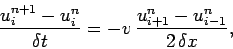 |
(236) |
where
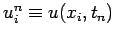 . The above equation can be rewritten
. The above equation can be rewritten
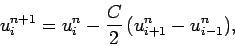 |
(237) |
where
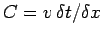 .
.
Let us perform a von Neumann stability analysis of the above differencing scheme.
Writing
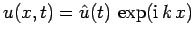 , we obtain
, we obtain
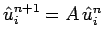 , where
, where
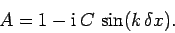 |
(238) |
Note that
 |
(239) |
Thus, the magnitude of the amplification factor is greater than unity for
all 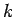 . This implies, unfortunately, that the simple differencing scheme (237)
is unconditionally unstable.
. This implies, unfortunately, that the simple differencing scheme (237)
is unconditionally unstable.



Next: The Lax scheme
Up: The wave equation
Previous: Introduction
Richard Fitzpatrick
2006-03-29
![]() ,
subject to the simple Dirichlet boundary conditions
,
subject to the simple Dirichlet boundary conditions
![]() .
As usual, we discretize in time on the uniform grid
.
As usual, we discretize in time on the uniform grid
![]() , for
, for
![]() .
Furthermore, in the
.
Furthermore, in the ![]() -direction, we discretize on the uniform grid
-direction, we discretize on the uniform grid
![]() , for
, for
![]() , where
, where
![]() . Adopting an explicit temporal differencing
scheme, and a centered spatial differencing scheme, Eq. (234) yields
. Adopting an explicit temporal differencing
scheme, and a centered spatial differencing scheme, Eq. (234) yields
![]() , we obtain
, we obtain
![]() , where
, where