


Next: 2-d problem with Neumann
Up: The diffusion equation
Previous: An improved 1-d solution
Let us consider the solution of the diffusion equation in two dimensions. Suppose
that
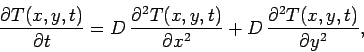 |
(214) |
for
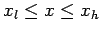 , and
, and 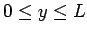 . Suppose that
. Suppose that 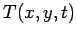 satisfies mixed
boundary conditions in the
satisfies mixed
boundary conditions in the  -direction:
-direction:
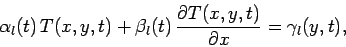 |
(215) |
at 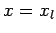 , and
, and
 |
(216) |
at 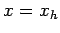 . Here,
. Here, 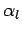 ,
,  , etc., are known functions of
, etc., are known functions of  ,
whereas
,
whereas 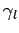 ,
, 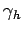 are known functions of
are known functions of  and
and  .
Furthermore, suppose that
.
Furthermore, suppose that 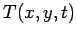 satisfies the following simple Dirichlet boundary
conditions in the
satisfies the following simple Dirichlet boundary
conditions in the  -direction:
-direction:
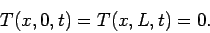 |
(217) |
As before, we discretize in time on the uniform grid
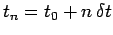 , for
, for
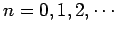 .
Furthermore, in the
.
Furthermore, in the  -direction, we discretize on the uniform grid
-direction, we discretize on the uniform grid
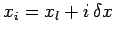 , for
, for
 , where
, where
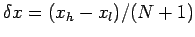 . Finally, in the
. Finally, in the  -direction, we discretize
on the uniform grid
-direction, we discretize
on the uniform grid
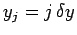 , for
, for 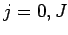 , where
, where
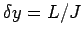 .
Adopting the Crank-Nicholson temporal differencing scheme discussed in Sect. 6.6, and
the second-order spatial differencing scheme outlined in
Sect. 5.2, Eq. (214) yields
.
Adopting the Crank-Nicholson temporal differencing scheme discussed in Sect. 6.6, and
the second-order spatial differencing scheme outlined in
Sect. 5.2, Eq. (214) yields
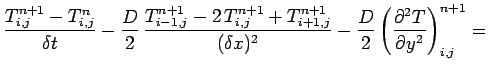 |
|
|
|
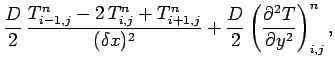 |
|
|
(218) |
where
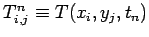 . The discretized boundary conditions
take the form
. The discretized boundary conditions
take the form
plus
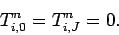 |
(221) |
Here,
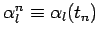 , etc., and
, etc., and
 , etc.
, etc.
Adopting the Fourier method introduced in Sect. 5.7, we
write the 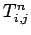 in terms of their Fourier-sine harmonics:
in terms of their Fourier-sine harmonics:
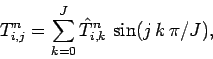 |
(222) |
which automatically satisfies the boundary conditions (221).
The above expression can be inverted to give (see Sect. 5.9)
 |
(223) |
When Eq. (218) is written in terms of the
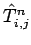 , it reduces to
, it reduces to
 |
|
|
|
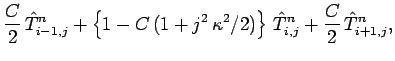 |
|
|
(224) |
for 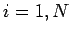 , and
, and 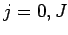 . Here,
. Here,
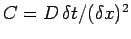 , and
, and
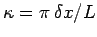 .
Moreover, the boundary conditions (219) and (220) yield
.
Moreover, the boundary conditions (219) and (220) yield
where
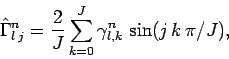 |
(227) |
etc. Equations (224)--(226) constitute a set of 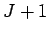 uncoupled tridiagonal matrix equations for the
uncoupled tridiagonal matrix equations for the
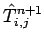 , with one
equation for each separate value of
, with one
equation for each separate value of  .
.
In order to advance our solution by one time-step, we first Fourier transform the
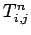 and the boundary conditions, according to Eqs. (223) and (227).
Next, we invert the
and the boundary conditions, according to Eqs. (223) and (227).
Next, we invert the 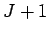 tridiagonal equations (224)--(226) to
obtain the
tridiagonal equations (224)--(226) to
obtain the
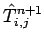 . Finally, we reconstruct the
. Finally, we reconstruct the 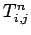 via
Eq. (222).
via
Eq. (222).



Next: 2-d problem with Neumann
Up: The diffusion equation
Previous: An improved 1-d solution
Richard Fitzpatrick
2006-03-29
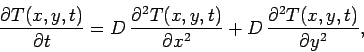
![]() , for
, for
![]() .
Furthermore, in the
.
Furthermore, in the ![]() -direction, we discretize on the uniform grid
-direction, we discretize on the uniform grid
![]() , for
, for
![]() , where
, where
![]() . Finally, in the
. Finally, in the ![]() -direction, we discretize
on the uniform grid
-direction, we discretize
on the uniform grid
![]() , for
, for ![]() , where
, where
![]() .
Adopting the Crank-Nicholson temporal differencing scheme discussed in Sect. 6.6, and
the second-order spatial differencing scheme outlined in
Sect. 5.2, Eq. (214) yields
.
Adopting the Crank-Nicholson temporal differencing scheme discussed in Sect. 6.6, and
the second-order spatial differencing scheme outlined in
Sect. 5.2, Eq. (214) yields
![]() in terms of their Fourier-sine harmonics:
in terms of their Fourier-sine harmonics:
![]() and the boundary conditions, according to Eqs. (223) and (227).
Next, we invert the
and the boundary conditions, according to Eqs. (223) and (227).
Next, we invert the ![]() tridiagonal equations (224)--(226) to
obtain the
tridiagonal equations (224)--(226) to
obtain the
![]() . Finally, we reconstruct the
. Finally, we reconstruct the ![]() via
Eq. (222).
via
Eq. (222).