


Next: 2-d problem with Dirichlet
Up: The diffusion equation
Previous: An improved 1-d diffusion
Let us now solve the simple diffusion problem introduced in Sect. 6.4 with the above listed
Crank-Nicholson routine. Figure 73
shows a comparison between the analytic and numerical solutions for
a calculation performed using 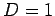 ,
,  ,
,  ,
,
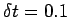 , and
, and 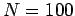 .
It can be seen that the analytic and numerical solutions are in excellent agreement.
Note, however, that the time-step used in this calculation (i.e.,
.
It can be seen that the analytic and numerical solutions are in excellent agreement.
Note, however, that the time-step used in this calculation (i.e.,
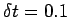 ) is much larger
than that used in our previous calculation (i.e.,
) is much larger
than that used in our previous calculation (i.e.,
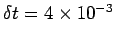 ), which employed an explicit differencing
scheme--see Fig. 71. According to Eq. (209), an explicit
scheme is limited to time-steps less than about
), which employed an explicit differencing
scheme--see Fig. 71. According to Eq. (209), an explicit
scheme is limited to time-steps less than about
 for the problem under
investigation.
Thus, we have been able to exceed this limit by a factor of 20 with our
implicit scheme, yet still maintain numerical stability.
Note that our Crank-Nicholson scheme is able to
obtain accurate results with a time-step as large as
for the problem under
investigation.
Thus, we have been able to exceed this limit by a factor of 20 with our
implicit scheme, yet still maintain numerical stability.
Note that our Crank-Nicholson scheme is able to
obtain accurate results with a time-step as large as 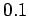 because it is
second-order in time.
because it is
second-order in time.
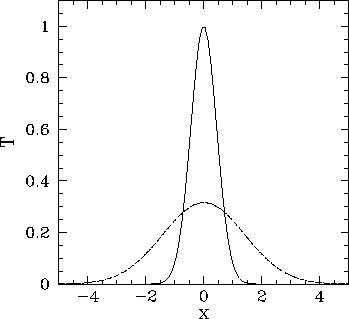
Figure 73:
Diffusive evolution of a 1-d Gaussian pulse.
Numerical calculation performed using
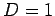 ,
,  ,
,
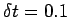 , and
, and 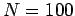 . The pulse is evolved from
. The pulse is evolved from 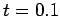 to
to 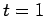 . The
solid curve shows the initial condition at
. The
solid curve shows the initial condition at 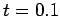 , the dashed curve the numerical solution
at
, the dashed curve the numerical solution
at 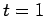 , and the dotted curve (obscured by the dashed curve) the analytic solution at
, and the dotted curve (obscured by the dashed curve) the analytic solution at 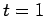 .
.
 |



Next: 2-d problem with Dirichlet
Up: The diffusion equation
Previous: An improved 1-d diffusion
Richard Fitzpatrick
2006-03-29

