


Next: The Crank-Nicholson scheme
Up: The diffusion equation
Previous: An example 1-d solution
Clearly, our simple finite difference algorithm
for solving the 1-d diffusion equation is subject to a numerical instability under certain circumstances.
Let us try to establish when this instability occurs. Consider the time evolution
of a single Fourier mode of wave-number 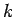 :
:
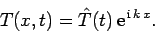 |
(204) |
Substitution of the above expression into our finite difference scheme (197) yields
![\begin{displaymath}
\hat{T}^{n+1}\,{\rm e}^{\,{\rm i}\,k\,x_n} = \hat{T}^n\,{\rm...
...m i}\,k\,\delta x}-2+ {\rm e}^{+{\rm i}\,k\,\delta x})\right],
\end{displaymath}](img871.png) |
(205) |
or
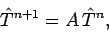 |
(206) |
where
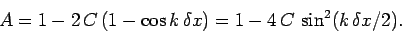 |
(207) |
Thus, the amplitude of the Fourier mode is amplified by a factor 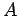 at each time-step.
In order for the differencing scheme to be stable, the
modulus of this amplification
factor must be less than unity for all possible values of
at each time-step.
In order for the differencing scheme to be stable, the
modulus of this amplification
factor must be less than unity for all possible values of 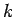 . Now, the largest
possible value of
. Now, the largest
possible value of
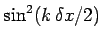 is unity: hence, the wave-length corresponding to
this value is that of the most unstable Fourier mode. In fact, the most unstable mode
possesses a wave-length which is half the grid-spacing: i.e.,
is unity: hence, the wave-length corresponding to
this value is that of the most unstable Fourier mode. In fact, the most unstable mode
possesses a wave-length which is half the grid-spacing: i.e.,
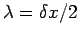 . It follows from Eq. (207) that this mode
is stable provided
. It follows from Eq. (207) that this mode
is stable provided
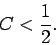 |
(208) |
Finally, from the definition of  , our stability condition can be written
, our stability condition can be written
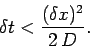 |
(209) |
Note that 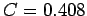 for the stable calculation shown in Fig. 71, whereas
for the stable calculation shown in Fig. 71, whereas 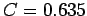 for the unstable calculation shown in Fig. 72.
Incidentally, the type of stability analysis outlined above is called von Neumann stability analysis.
Note that the neglect of the spatial boundary conditions in the above calculation is justified
because the unstable modes vary on very small length-scales which are typically of order the grid spacing.
for the unstable calculation shown in Fig. 72.
Incidentally, the type of stability analysis outlined above is called von Neumann stability analysis.
Note that the neglect of the spatial boundary conditions in the above calculation is justified
because the unstable modes vary on very small length-scales which are typically of order the grid spacing.
According to Eq. (209), our finite difference scheme for solving the 1-d diffusion
equation is only stable provided that the time-step remains below some critical value.
Note that this critical value scales like the square of the grid-spacing. This is
a very unfavorable scaling, since it implies that a doubling of the spatial resolution
requires a simultaneous reduction
in the time-step by a factor of four in order to maintain numerical stability.
Certainly, the above constraint limits us to absurdly small time-steps in high resolution
calculations.
Is there any way of overcoming this constraint?



Next: The Crank-Nicholson scheme
Up: The diffusion equation
Previous: An example 1-d solution
Richard Fitzpatrick
2006-03-29