


Next: von Neumann stability analysis
Up: The diffusion equation
Previous: An example 1-d diffusion
An example 1-d solution of the diffusion equation
Let us now solve the diffusion equation in 1-d using the finite difference
technique discussed above. We seek the solution of Eq. (191)
in the region
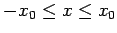 , subject to the initial
condition
, subject to the initial
condition
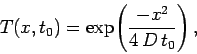 |
(200) |
where 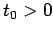 . The spatial boundary conditions are
. The spatial boundary conditions are
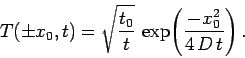 |
(201) |
Of course, we can solve this problem
analytically to give
 |
(202) |
Note that the above equation describes a Gaussian
pulse which gradually decreases in height
and broadens in width in such a manner that its area is conserved. The width of the pulse
varies approximately as
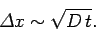 |
(203) |
Moreover, the pulse approaches a 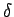 -function as
-function as
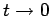 .
.
Figure 71:
Diffusive evolution of a 1-d Gaussian pulse.
Numerical calculation performed using
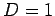 ,
,  ,
,
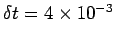 , and
, and 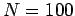 . The pulse is evolved from
. The pulse is evolved from 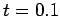 to
to 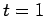 . The
solid curve shows the initial condition at
. The
solid curve shows the initial condition at 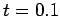 , the dashed curve the numerical solution
at
, the dashed curve the numerical solution
at 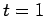 , and the dotted curve (obscured by the dashed curve) the analytic solution at
, and the dotted curve (obscured by the dashed curve) the analytic solution at 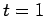 .
.
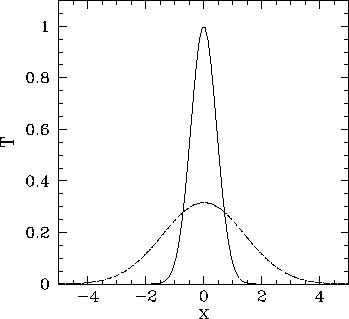 |
Figure 71 shows a comparison between the analytic and numerical solutions for
a calculation performed using 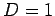 ,
,  ,
,  ,
,
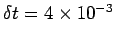 , and
, and 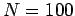 .
It can be seen that the analytic and numerical solutions are in excellent agreement.
.
It can be seen that the analytic and numerical solutions are in excellent agreement.
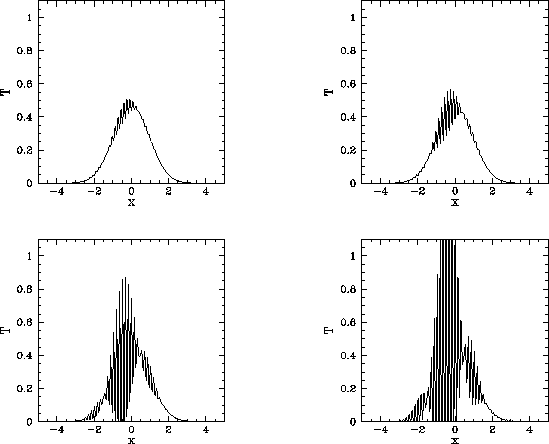
Figure 72:
Diffusive evolution of a 1-d Gaussian pulse.
Numerical calculation performed using
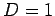 ,
,  ,
,
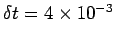 , and
, and 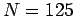 . The simulation is started
at
. The simulation is started
at 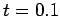 . The top-left, top-right, bottom-left, and bottom-right panels
show the solution at
. The top-left, top-right, bottom-left, and bottom-right panels
show the solution at 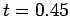 ,
,  ,
, 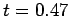 , and
, and 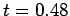 , respectively.
, respectively.
 |
It is reasonable to expect that as  increases at fixed
increases at fixed 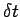 (i.e., the spatial resolution increases at fixed temporal resolution) the numerical
solution should become more and more accurate. This is indeed the case--at least, until
(i.e., the spatial resolution increases at fixed temporal resolution) the numerical
solution should become more and more accurate. This is indeed the case--at least, until  exceeds a critical value. Beyond this value, there is a
catastrophic breakdown in the numerical solution. This breakdown is illustrated in Fig. 72.
It can be seen that the
solution develops rapidly growing short-wavelength oscillations. Indeed, the solution
eventually becomes effectively infinite. Let us investigate this unusual
and rather disturbing phenomenon.
exceeds a critical value. Beyond this value, there is a
catastrophic breakdown in the numerical solution. This breakdown is illustrated in Fig. 72.
It can be seen that the
solution develops rapidly growing short-wavelength oscillations. Indeed, the solution
eventually becomes effectively infinite. Let us investigate this unusual
and rather disturbing phenomenon.



Next: von Neumann stability analysis
Up: The diffusion equation
Previous: An example 1-d diffusion
Richard Fitzpatrick
2006-03-29
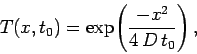
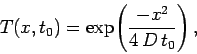
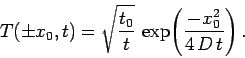


![]() ,
, ![]() ,
, ![]() ,
,
![]() , and
, and ![]() .
It can be seen that the analytic and numerical solutions are in excellent agreement.
.
It can be seen that the analytic and numerical solutions are in excellent agreement.

![]() increases at fixed
increases at fixed ![]() (i.e., the spatial resolution increases at fixed temporal resolution) the numerical
solution should become more and more accurate. This is indeed the case--at least, until
(i.e., the spatial resolution increases at fixed temporal resolution) the numerical
solution should become more and more accurate. This is indeed the case--at least, until ![]() exceeds a critical value. Beyond this value, there is a
catastrophic breakdown in the numerical solution. This breakdown is illustrated in Fig. 72.
It can be seen that the
solution develops rapidly growing short-wavelength oscillations. Indeed, the solution
eventually becomes effectively infinite. Let us investigate this unusual
and rather disturbing phenomenon.
exceeds a critical value. Beyond this value, there is a
catastrophic breakdown in the numerical solution. This breakdown is illustrated in Fig. 72.
It can be seen that the
solution develops rapidly growing short-wavelength oscillations. Indeed, the solution
eventually becomes effectively infinite. Let us investigate this unusual
and rather disturbing phenomenon.