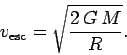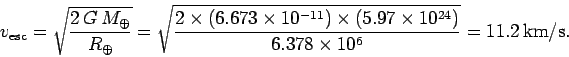Next: Satellite orbits
Up: Orbital motion
Previous: Gravity
We saw earlier, in Sect. 5.5, that gravity is a conservative force, and, therefore,
has an associated potential energy. Let us obtain a general formula for this energy.
Consider a point object of mass  , which is a radial distance
, which is a radial distance  from another point
object of mass
from another point
object of mass  . The gravitational force acting on the first mass is
of magnitude
. The gravitational force acting on the first mass is
of magnitude  , and is directed towards the second mass. Imagine that the
first mass moves radially away from the second mass, until it reaches infinity. What is
the change in the potential energy of the first mass associated with this shift?
According to Eq. (155),
, and is directed towards the second mass. Imagine that the
first mass moves radially away from the second mass, until it reaches infinity. What is
the change in the potential energy of the first mass associated with this shift?
According to Eq. (155),
![\begin{displaymath}
U(\infty) - U(r) = -\int_{r}^\infty [-f(r)] dr.
\end{displaymath}](img1936.png) |
(550) |
There is a minus sign in front of 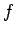 because this force is oppositely directed to the motion.
The above expression can be integrated to give
because this force is oppositely directed to the motion.
The above expression can be integrated to give
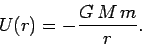 |
(551) |
Here, we have adopted the convenient normalization that the potential energy at infinity is
zero. According to the above formula, the gravitational potential energy of a mass  located a distance
located a distance  from a mass
from a mass  is simply
is simply  .
.
Consider an object of mass  moving close to the Earth's surface. The potential
energy of such an object can be written
moving close to the Earth's surface. The potential
energy of such an object can be written
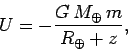 |
(552) |
where 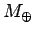 and
and  are the mass and radius of the Earth, respectively, and
are the mass and radius of the Earth, respectively, and
 is the vertical height of the object above the Earth's surface. In the limit that
is the vertical height of the object above the Earth's surface. In the limit that
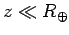 , the above expression can be expanded using the binomial theorem
to give
, the above expression can be expanded using the binomial theorem
to give
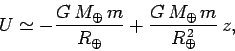 |
(553) |
Since potential energy is undetermined to an arbitrary additive constant, we could just as
well write
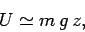 |
(554) |
where
 is the acceleration due to gravity at
the Earth's surface [see Eq. (548)]. Of course, the above formula is equivalent
to the formula (125) derived earlier on in this course.
is the acceleration due to gravity at
the Earth's surface [see Eq. (548)]. Of course, the above formula is equivalent
to the formula (125) derived earlier on in this course.
For an object of mass  and speed
and speed  , moving in the gravitational field of a fixed object
of mass
, moving in the gravitational field of a fixed object
of mass  , we expect the total energy,
, we expect the total energy,
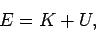 |
(555) |
to be a constant of the motion. Here, the kinetic energy is written
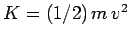 , whereas
the potential energy takes the form
, whereas
the potential energy takes the form
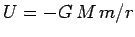 . Of course,
. Of course,  is the distance between the
two objects. Suppose that the fixed object is a sphere of radius
is the distance between the
two objects. Suppose that the fixed object is a sphere of radius  . Suppose,
further, that the second object is launched from the surface of this sphere
with some velocity
. Suppose,
further, that the second object is launched from the surface of this sphere
with some velocity  which is such that it only just escapes the sphere's gravitational
influence. After the object has escaped, it is a long way away from the sphere, and hence
which is such that it only just escapes the sphere's gravitational
influence. After the object has escaped, it is a long way away from the sphere, and hence
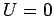 . Moreover, if the object only just escaped, then we also expect
. Moreover, if the object only just escaped, then we also expect 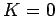 , since the
object will have expended all of its initial kinetic energy escaping from the sphere's
gravitational well. We conclude that our object possesses zero net energy:
i.e.,
, since the
object will have expended all of its initial kinetic energy escaping from the sphere's
gravitational well. We conclude that our object possesses zero net energy:
i.e., 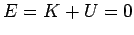 . Since
. Since 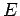 is a constant of the motion, it follows
that at the launch point
is a constant of the motion, it follows
that at the launch point
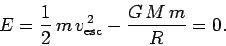 |
(556) |
This expression can be rearranged to give
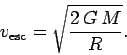 |
(557) |
The quantity  is known as the escape velocity. Objects launched from
the surface of the sphere with velocities exceeding this value will eventually
escape from the sphere's gravitational influence. Otherwise, the objects
will remain in orbit around the sphere, and may eventually strike its surface.
Note that the escape velocity is independent of the object's mass and launch
direction (assuming that it is not straight into the sphere).
is known as the escape velocity. Objects launched from
the surface of the sphere with velocities exceeding this value will eventually
escape from the sphere's gravitational influence. Otherwise, the objects
will remain in orbit around the sphere, and may eventually strike its surface.
Note that the escape velocity is independent of the object's mass and launch
direction (assuming that it is not straight into the sphere).
The escape velocity for the Earth is
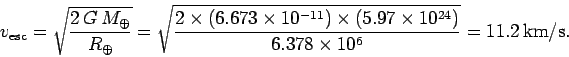 |
(558) |
Clearly, NASA must launch deep space probes from the surface of the Earth with velocities which exceed this value if they are
to have any hope of eventually reaching their targets.



Next: Satellite orbits
Up: Orbital motion
Previous: Gravity
Richard Fitzpatrick
2006-02-02
![]() moving close to the Earth's surface. The potential
energy of such an object can be written
moving close to the Earth's surface. The potential
energy of such an object can be written
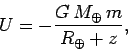
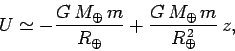
![]() and speed
and speed ![]() , moving in the gravitational field of a fixed object
of mass
, moving in the gravitational field of a fixed object
of mass ![]() , we expect the total energy,
, we expect the total energy,