| (123) |
| (126) |
Incidentally, the expressions (124) and (125) for kinetic and gravitational potential energy, respectively, are quite general, and do not just apply to free-fall under gravity. The mks unit of energy is called the joule (symbol J). In fact, 1 joule is equivalent to 1 kilogram meter-squared per second-squared, or 1 newton-meter. Note that all forms of energy are measured in the same units (otherwise the idea of energy conservation would make no sense).
One of the most important lessons which students learn during their studies
is that there are generally many different paths to the same
result in physics. Now, we have already analyzed free-fall under gravity using Newton's
laws of motion. However, it is illuminating to re-examine this problem from the
point of view of energy conservation. Suppose that a mass ![]() is dropped from rest and
falls a distance
is dropped from rest and
falls a distance ![]() . What is the final velocity
. What is the final velocity ![]() of the mass? Well,
according to Eq. (123), if energy is conserved then
of the mass? Well,
according to Eq. (123), if energy is conserved then
| (128) |
| (129) |
Suppose that the same mass is thrown upwards with initial velocity ![]() . What is the
maximum height
. What is the
maximum height ![]() to which it rises? Well, it is clear from Eq. (125) that as
the mass rises its potential energy increases. It, therefore, follows from
energy conservation that its kinetic energy must decrease with height. Note, however,
from Eq. (124), that kinetic energy can never be negative (since it
is the product of the two positive definite quantities,
to which it rises? Well, it is clear from Eq. (125) that as
the mass rises its potential energy increases. It, therefore, follows from
energy conservation that its kinetic energy must decrease with height. Note, however,
from Eq. (124), that kinetic energy can never be negative (since it
is the product of the two positive definite quantities, ![]() and
and ![]() ). Hence, once the
mass has risen to a height
). Hence, once the
mass has risen to a height ![]() which is such that its kinetic energy is reduced to zero
it can rise no further, and must, presumably, start to fall. The change in potential
energy of the mass in moving from its initial height to its maximum height is
which is such that its kinetic energy is reduced to zero
it can rise no further, and must, presumably, start to fall. The change in potential
energy of the mass in moving from its initial height to its maximum height is
![]() . The corresponding change in kinetic energy is
. The corresponding change in kinetic energy is
![]() ; since
; since
![]() is the initial kinetic energy, and the final kinetic energy is zero.
It follows from Eq. (127) that
is the initial kinetic energy, and the final kinetic energy is zero.
It follows from Eq. (127) that
![]() , which can be
rearranged to give
, which can be
rearranged to give
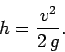 |
(130) |
It should be noted that the idea of energy conservation--although extremely useful--is not a replacement for Newton's laws of motion. For instance, in the previous example, there is no way in which we can deduce how long it takes the mass to rise to its maximum height from energy conservation alone--this information can only come from the direct application of Newton's laws.