This is, perhaps,
an appropriate point at which to note that the concept of gravitational potential energy--although
extremely useful--is, strictly speaking, fictitious.
To be more exact, the potential energy of a body is not
an intrinsic property of that body (unlike its kinetic energy). In fact, the
gravitational potential energy of
a given body is stored in the gravitational field which surrounds it. Thus,
when the body rises, and its potential energy consequently increases by an amount
![]() ; in reality, it is
the energy of the gravitational field surrounding the body which increases by this amount.
Of course, the increase in energy of the gravitational field is offset by a corresponding decrease in the
body's kinetic energy. Thus, when we speak of a body's kinetic energy being transformed
into potential energy, we are really talking about a flow of energy from the body to
the surrounding gravitational field. This energy flow is mediated by the
gravitational force exerted by the field on the body in question.
; in reality, it is
the energy of the gravitational field surrounding the body which increases by this amount.
Of course, the increase in energy of the gravitational field is offset by a corresponding decrease in the
body's kinetic energy. Thus, when we speak of a body's kinetic energy being transformed
into potential energy, we are really talking about a flow of energy from the body to
the surrounding gravitational field. This energy flow is mediated by the
gravitational force exerted by the field on the body in question.
Incidentally, according to Einstein's general theory of relativity (1917), the gravitational field of a mass consists of the local distortion that mass induces in the fabric of space-time. Fortunately, however, we do not need to understand general relativity in order to talk about gravitational fields or gravitational potential energy. All we need to know is that a gravitational field stores energy without loss: i.e., if a given mass rises a certain distance, and, thereby, gives up a certain amount of energy to the surrounding gravitational field, then that field will return this energy to the mass--without loss--if the mass falls by the same distance. In physics, we term such a field a conservative field (see later).
Suppose that a mass ![]() falls a distance
falls a distance ![]() . During this process, the energy of
the gravitational field decreases by a certain amount (i.e., the fictitious
potential energy of the mass decreases by a certain amount), and the body's
kinetic energy increases by a corresponding amount. This transfer of
energy, from the field to the mass,
is, presumably, mediated by the gravitational force
. During this process, the energy of
the gravitational field decreases by a certain amount (i.e., the fictitious
potential energy of the mass decreases by a certain amount), and the body's
kinetic energy increases by a corresponding amount. This transfer of
energy, from the field to the mass,
is, presumably, mediated by the gravitational force ![]() (the minus sign
indicates that the force is directed downwards) acting on the mass. In fact,
given that
(the minus sign
indicates that the force is directed downwards) acting on the mass. In fact,
given that ![]() , it follows from Eq. (127) that
, it follows from Eq. (127) that
In physics, we generally refer to the
amount of energy transferred to a body, when a force acts upon it, as
the amount of work ![]() performed by that force on the body in question. It follows from
Eq. (131) that when a gravitational force
performed by that force on the body in question. It follows from
Eq. (131) that when a gravitational force ![]() acts on a body,
causing it to displace a distance
acts on a body,
causing it to displace a distance ![]() in the direction of that force,
then the net work done on the body is
in the direction of that force,
then the net work done on the body is
In deriving equation (132), we have made two assumptions which are not universally
valid. Firstly, we have assumed that the motion of the body upon which the force acts is
both 1-dimensional and parallel to the line of action of the force.
Secondly, we have assumed that the force does not vary with position.
Let us attempt to relax these two assumptions, so as to obtain an expression for the
work ![]() done by a general force
done by a general force ![]() .
.
Let us start by relaxing the first assumption. Suppose, for the sake of argument, that
we have a mass ![]() which moves under gravity in 2-dimensions. Let us adopt
the coordinate system shown in Fig. 35, with
which moves under gravity in 2-dimensions. Let us adopt
the coordinate system shown in Fig. 35, with ![]() representing vertical
distance, and
representing vertical
distance, and ![]() representing horizontal distance. The vector
acceleration of the mass is simply
representing horizontal distance. The vector
acceleration of the mass is simply
![]() . Here, we are neglecting the redundant
. Here, we are neglecting the redundant
![]() -component, for the sake of simplicity. The physics of motion under gravity in more
than 1-dimension is summarized by the three equations (64)-(66). Let us examine
the last of these equations:
-component, for the sake of simplicity. The physics of motion under gravity in more
than 1-dimension is summarized by the three equations (64)-(66). Let us examine
the last of these equations:
| (133) |
| (135) |
Let us now try to relate the flow of energy between the gravitational field and the mass
to the action of the gravitational force,
![]() . Equation (134)
can be rewritten
. Equation (134)
can be rewritten
Figure 36 is a visualization of the definition (136). The work ![]() performed by a force
performed by a force ![]() when the object upon which it acts is subject to a displacement
when the object upon which it acts is subject to a displacement
![]() is
is
| (137) |
Suppose, now, that an object is subject to a force ![]() which varies with position. What
is the total work done by the force when the object moves along some
general trajectory in space between points
which varies with position. What
is the total work done by the force when the object moves along some
general trajectory in space between points ![]() and
and ![]() (say)? See Fig. 37.
Well, one way in which we could approach this problem would be to approximate the trajectory
as a series of
(say)? See Fig. 37.
Well, one way in which we could approach this problem would be to approximate the trajectory
as a series of ![]() straight-line segments, as shown in Fig. 38. Suppose that the
vector displacement of the
straight-line segments, as shown in Fig. 38. Suppose that the
vector displacement of the ![]() th segment is
th segment is
![]() . Suppose, further,
that
. Suppose, further,
that ![]() is sufficiently large that the force
is sufficiently large that the force ![]() does not vary much
along each segment. In fact, let the average force along the
does not vary much
along each segment. In fact, let the average force along the ![]() th segment be
th segment be
![]() . We shall assume that formula (136)--which is valid for constant
forces and straight-line displacements--holds good for each segment. It follows that
the net work done on the body, as it moves from point
. We shall assume that formula (136)--which is valid for constant
forces and straight-line displacements--holds good for each segment. It follows that
the net work done on the body, as it moves from point ![]() to
point
to
point ![]() , is approximately
, is approximately
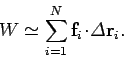 |
(138) |
The meaning of Eq. (139) becomes a lot clearer if we restrict our
attention to 1-dimensional motion. Suppose, therefore, that an object moves
in 1-dimension, with displacement ![]() , and is subject to a varying force
, and is subject to a varying force ![]() (directed along the
(directed along the ![]() -axis). What is the work done by this force when
the object moves from
-axis). What is the work done by this force when
the object moves from ![]() to
to ![]() ? Well, a straight-forward
application of Eq. (139) [with
? Well, a straight-forward
application of Eq. (139) [with
![]() and
and
![]() ]
yields
]
yields
Let us, finally, round-off this discussion by re-deriving the so-called work-energy theorem,
Eq. (136), in 1-dimension, allowing for a non-constant force.
According to Newton's second law of motion,
![\begin{displaymath}
W = \int_{x_A}^{x_B} m \frac{d^2 x}{dt^2} dx = \int_{t_A}^...
...}\!\left[\frac{m}{2}\!\left(\frac{dx}{dt}\right)^2\right] dt,
\end{displaymath}](img634.png) |
(142) |
| (143) |
Suppose, finally, that an object is subject to more than one force. How do we calculate the
net work ![]() performed by all these forces as the object moves from point
performed by all these forces as the object moves from point ![]() to
point
to
point ![]() ? One approach would be to calculate the work done by each force, taken
in isolation, and then to sum the results. In other words, defining
? One approach would be to calculate the work done by each force, taken
in isolation, and then to sum the results. In other words, defining
| (144) |
| (145) |
| (146) |
| (147) |