


Next: Potential energy
Up: Conservation of energy
Previous: Work
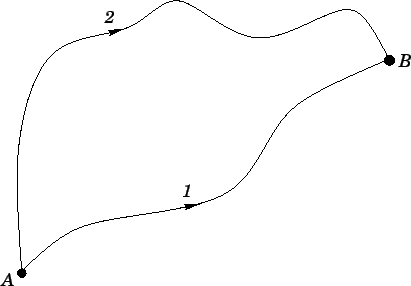
Suppose that a non-uniform force-field
 acts upon
an object which moves along a curved trajectory, labeled path 1, from point
acts upon
an object which moves along a curved trajectory, labeled path 1, from point  to
point
to
point  . See Fig. 40. As we have seen, the work
. See Fig. 40. As we have seen, the work 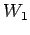 performed by the force-field
on the object can be written as a line-integral along this trajectory:
performed by the force-field
on the object can be written as a line-integral along this trajectory:
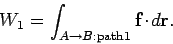 |
(148) |
Suppose that the same object moves along a different trajectory, labeled path
2, between the same two points. In this case, the work 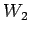 performed by the force-field is
performed by the force-field is
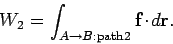 |
(149) |
Basically, there are two possibilities. Firstly, the line-integrals (148) and
(149) might depend on the end points,  and
and  , but not on the path
taken between them, in which case
, but not on the path
taken between them, in which case 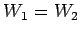 . Secondly, the line-integrals (148) and
(149) might depend both on the end points,
. Secondly, the line-integrals (148) and
(149) might depend both on the end points,  and
and  , and the path
taken between them, in which case
, and the path
taken between them, in which case 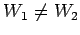 (in general). The first possibility
corresponds to what physicists term a conservative force-field, whereas the
second possibility corresponds to a non-conservative force-field.
(in general). The first possibility
corresponds to what physicists term a conservative force-field, whereas the
second possibility corresponds to a non-conservative force-field.
Figure 40:
Two alternative paths between points  and
and 
 |
What is the physical distinction between a conservative and a non-conservative
force-field? Well, the easiest way of answering this question is to
slightly modify the problem discussed above. Suppose, now, that the object moves from
point  to point
to point  along path 1, and then from point
along path 1, and then from point  back to point
back to point  along path 2. What is the total work done on the object by the force-field as
it executes this closed circuit? Incidentally, one fact which should be clear from the
definition of a line-integral is that if we simply reverse the path of a given
integral then the value of that integral picks up a minus sign: in other
words,
along path 2. What is the total work done on the object by the force-field as
it executes this closed circuit? Incidentally, one fact which should be clear from the
definition of a line-integral is that if we simply reverse the path of a given
integral then the value of that integral picks up a minus sign: in other
words,
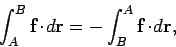 |
(150) |
where it is understood that both the above integrals are taken in opposite directions
along the same path. Recall that conventional 1-dimensional integrals
obey an analogous rule: i.e., if we swap the limits of
integration then the integral picks up a minus sign.
It follows that the total work done on the object as it executes
the circuit is simply
 |
(151) |
where 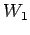 and
and 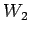 are defined in Eqs. (148) and (149), respectively.
There is a minus sign in front of
are defined in Eqs. (148) and (149), respectively.
There is a minus sign in front of 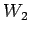 because we are moving from point
because we are moving from point  to point
to point
 , instead of the other way around. For the case of a conservative field, we have
, instead of the other way around. For the case of a conservative field, we have
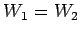 . Hence, we conclude that
. Hence, we conclude that
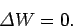 |
(152) |
In other words, the net work done by a conservative field on an object taken around
a closed loop is zero. This is just another way of saying that a conservative
field stores energy without loss: i.e., if an object gives up a
certain amount of energy to a conservative field in traveling from point  to point
to point  , then the
field returns this energy to the object--without loss--when it travels back
to point
, then the
field returns this energy to the object--without loss--when it travels back
to point  . For the case of a non-conservative field,
. For the case of a non-conservative field, 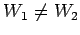 . Hence, we
conclude that
. Hence, we
conclude that
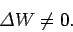 |
(153) |
In other words, the net work done by a non-conservative field on an object taken around
a closed loop is non-zero. In practice, the net work is invariably negative.
This is just another way of saying that a non-conservative field dissipates energy:
i.e., if an object gives up a
certain amount of energy to a non-conservative field in traveling from point  to point
to point  , then the
field only returns part, or, perhaps, none, of this energy to the object when it travels back
to point
, then the
field only returns part, or, perhaps, none, of this energy to the object when it travels back
to point  . The remainder is usually dissipated as heat.
. The remainder is usually dissipated as heat.
What are typical examples of conservative and non-conservative fields? Well, a gravitational
field is probably the most well-known example of a conservative field (see later).
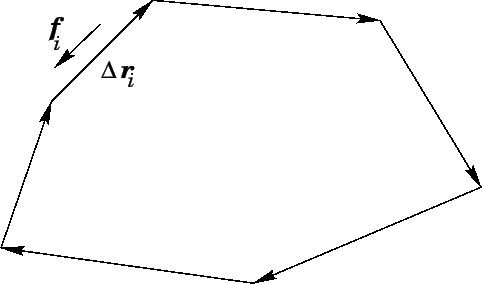
A typical example of a non-conservative field might consist of an
object moving over a rough horizontal surface. Suppose, for the sake of simplicity,
that the object executes a closed circuit on the surface which is made
up entirely of straight-line segments, as shown in Fig. 41.
Let
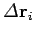 represent the vector displacement of the
represent the vector displacement of the  th leg
of this circuit. Suppose that the frictional force acting on the object as it executes this
leg is
th leg
of this circuit. Suppose that the frictional force acting on the object as it executes this
leg is 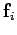 . One thing that we know about a frictional force
is that it is always directed in the opposite direction to the instantaneous
direction of motion of the object upon which it acts. Hence,
. One thing that we know about a frictional force
is that it is always directed in the opposite direction to the instantaneous
direction of motion of the object upon which it acts. Hence,
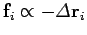 . It follows that
. It follows that
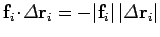 . Thus, the net work
performed by the frictional force on the object, as it executes the circuit, is
given by
. Thus, the net work
performed by the frictional force on the object, as it executes the circuit, is
given by
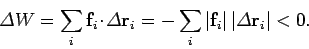 |
(154) |
The fact that the net work is negative indicates that the frictional force continually
drains energy from the object as it moves over the surface. This energy
is actually dissipated as heat (we all know that if we rub two rough surfaces
together, sufficiently vigorously, then they will eventually heat up: this is
how mankind first made fire) and is, therefore, lost to the
system. (Generally speaking, the laws of thermodynamics forbid energy which has been
converted into heat from being converted back to its original form.)
Hence, friction is an example of a non-conservative force, because it dissipates
energy rather than storing it.
Figure 41:
Closed circuit over a rough horizontal surface
 |



Next: Potential energy
Up: Conservation of energy
Previous: Work
Richard Fitzpatrick
2006-02-02
![]() to point
to point ![]() along path 1, and then from point
along path 1, and then from point ![]() back to point
back to point ![]() along path 2. What is the total work done on the object by the force-field as
it executes this closed circuit? Incidentally, one fact which should be clear from the
definition of a line-integral is that if we simply reverse the path of a given
integral then the value of that integral picks up a minus sign: in other
words,
along path 2. What is the total work done on the object by the force-field as
it executes this closed circuit? Incidentally, one fact which should be clear from the
definition of a line-integral is that if we simply reverse the path of a given
integral then the value of that integral picks up a minus sign: in other
words,
![]() represent the vector displacement of the
represent the vector displacement of the ![]() th leg
of this circuit. Suppose that the frictional force acting on the object as it executes this
leg is
th leg
of this circuit. Suppose that the frictional force acting on the object as it executes this
leg is ![]() . One thing that we know about a frictional force
is that it is always directed in the opposite direction to the instantaneous
direction of motion of the object upon which it acts. Hence,
. One thing that we know about a frictional force
is that it is always directed in the opposite direction to the instantaneous
direction of motion of the object upon which it acts. Hence,
![]() . It follows that
. It follows that
![]() . Thus, the net work
performed by the frictional force on the object, as it executes the circuit, is
given by
. Thus, the net work
performed by the frictional force on the object, as it executes the circuit, is
given by