


Next: Hooke's law
Up: Conservation of energy
Previous: Conservative and non-conservative force-fields
Potential energy
Consider a body moving in a conservative force-field
 . Let us
arbitrarily pick some point
. Let us
arbitrarily pick some point  in this field. We can define a
function
in this field. We can define a
function 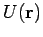 which possesses a unique value at every point in
the field. The value of this function associated with some
general point
which possesses a unique value at every point in
the field. The value of this function associated with some
general point  is simply
is simply
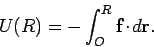 |
(155) |
In other words, 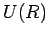 is just the energy transferred to the field (i.e., minus
the work done by the field) when the
body moves from point
is just the energy transferred to the field (i.e., minus
the work done by the field) when the
body moves from point  to point
to point  . Of course, the value of
. Of course, the value of 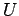 at point
at point
 is zero: i.e.,
is zero: i.e.,  . Note that the above definition uniquely specifies
. Note that the above definition uniquely specifies 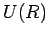 , since
the work done when a body moves between two points in a conservative
force-field is independent of the path taken between these points. Furthermore,
the above definition would make no sense in a non-conservative field, since
the work done when a body moves between two points in such a
field is dependent on the chosen path: hence,
, since
the work done when a body moves between two points in a conservative
force-field is independent of the path taken between these points. Furthermore,
the above definition would make no sense in a non-conservative field, since
the work done when a body moves between two points in such a
field is dependent on the chosen path: hence, 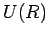 would have an infinite number
of different values corresponding to the infinite number of different paths the body could take
between points
would have an infinite number
of different values corresponding to the infinite number of different paths the body could take
between points  and
and  .
.
According to the work-energy theorem,
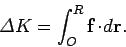 |
(156) |
In other words, the net change in the kinetic energy of the body, as it
moves from point  to point
to point  , is equal to the work done
on the body by the force-field during this process.
However, comparing with Eq. (155), we can see that
, is equal to the work done
on the body by the force-field during this process.
However, comparing with Eq. (155), we can see that
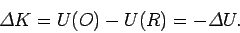 |
(157) |
In other words, the increase in the kinetic energy of the body, as it moves
from point  to point
to point  , is equal to the decrease in the
function
, is equal to the decrease in the
function 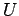 evaluated between these same two points. Another way
of putting this is
evaluated between these same two points. Another way
of putting this is
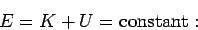 |
(158) |
i.e., the sum of the kinetic energy and the function 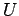 remains
constant as the body moves around in the force-field. It should be clear, by now, that the
function
remains
constant as the body moves around in the force-field. It should be clear, by now, that the
function 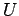 represents some form of potential energy.
represents some form of potential energy.
The above discussion leads to the following important conclusions. Firstly,
it should be possible to associate a potential energy (i.e., an energy
a body possesses by virtue of its position) with any conservative
force-field. Secondly, any force-field for which we can define
a potential energy must necessarily be conservative. For instance, the existence
of gravitational potential energy is proof that gravitational fields
are conservative.
Thirdly, the concept of potential energy is meaningless
in a non-conservative force-field (since the potential energy at a
given point cannot be uniquely defined). Fourthly, potential energy is
only defined to within an arbitrary additive constant. In other words,
the point in space at which we set the potential energy to zero
can be chosen at will. This implies that only differences in potential
energies between different points in space have any physical
significance. For instance, we have seen that the definition of
gravitational potential energy is 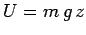 , where
, where  represents height above
the ground. However, we could just as well write
represents height above
the ground. However, we could just as well write
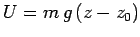 , where
, where
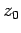 is the height of some arbitrarily chosen reference point
(e.g., the top of Mount Everest, or the bottom of the
Dead Sea). Fifthly, the difference in potential energy between two points
represents the net energy transferred to the associated force-field when a body moves
between these two points. In other words, potential energy is not, strictly speaking, a
property of the body--instead, it is a property of the force-field within which
the body moves.
is the height of some arbitrarily chosen reference point
(e.g., the top of Mount Everest, or the bottom of the
Dead Sea). Fifthly, the difference in potential energy between two points
represents the net energy transferred to the associated force-field when a body moves
between these two points. In other words, potential energy is not, strictly speaking, a
property of the body--instead, it is a property of the force-field within which
the body moves.



Next: Hooke's law
Up: Conservation of energy
Previous: Conservative and non-conservative force-fields
Richard Fitzpatrick
2006-02-02
![]() , where
, where ![]() represents height above
the ground. However, we could just as well write
represents height above
the ground. However, we could just as well write
![]() , where
, where
![]() is the height of some arbitrarily chosen reference point
(e.g., the top of Mount Everest, or the bottom of the
Dead Sea). Fifthly, the difference in potential energy between two points
represents the net energy transferred to the associated force-field when a body moves
between these two points. In other words, potential energy is not, strictly speaking, a
property of the body--instead, it is a property of the force-field within which
the body moves.
is the height of some arbitrarily chosen reference point
(e.g., the top of Mount Everest, or the bottom of the
Dead Sea). Fifthly, the difference in potential energy between two points
represents the net energy transferred to the associated force-field when a body moves
between these two points. In other words, potential energy is not, strictly speaking, a
property of the body--instead, it is a property of the force-field within which
the body moves.