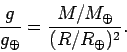Next: Gravitational potential energy
Up: Orbital motion
Previous: Historical background
There is one important question which we have avoided discussing until now. Why do objects fall towards the
surface of the Earth? The ancient Greeks had a very simple answer to this question.
According to Aristotle, all objects have a natural tendency to fall towards the centre of
the Universe. Since the centre of the Earth coincides with the centre of the Universe, all objects also
tend to fall towards the Earth's surface. So, an ancient Greek might ask, why do the planets
not fall towards the Earth? Well, according to Aristotle, the planets are embedded in crystal
spheres which rotate with them whilst holding them in place in the firmament. Unfortunately,
Ptolemy seriously undermined this explanation by shifting the Earth slightly from the
centre of the Universe. However, the coup de grace was delivered by Copernicus,
who converted the Earth into just another planet orbiting the Sun.
So, why do objects fall towards the surface of the Earth? The first person, after Aristotle, to seriously
consider this question was Sir Isaac Newton. Since the Earth is not located in a special
place in the Universe, Newton reasoned, objects must be attracted toward the Earth itself.
Moreover, since the Earth is just another planet, objects must be attracted towards other
planets as well. In fact, all objects must exert a force of attraction on all
other objects in the Universe. What intrinsic property of objects causes them
to exert this attractive force--which Newton termed gravity--on other objects? Newton decided that the
crucial property was mass. After much thought, he was eventually able to
formulate his famous law of universal gravitation:
Every particle in the Universe attracts every other particle with a
force directly proportional to the product of their masses and inversely
proportional to the square of the distance between them. The direction
of the force is along the line joining the particles.
Incidentally, Newton adopted an inverse square law because he knew that this was the
only type of force law which was consistent with Kepler's third law of planetary motion.
Consider two point
objects of masses 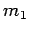 and
and 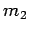 , separated by a distance
, separated by a distance  .
As illustrated in Fig. 104, the magnitude of the force of attraction
between these objects is
.
As illustrated in Fig. 104, the magnitude of the force of attraction
between these objects is
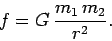 |
(541) |
The direction of the force is along the line joining the two objects.
Figure 104:
Newton's law of gravity.
 |
Let 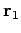 and
and 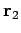 be the vector positions of the two objects,
respectively. The vector gravitational force exerted by object 2 on object 1 can
be written
be the vector positions of the two objects,
respectively. The vector gravitational force exerted by object 2 on object 1 can
be written
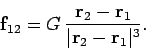 |
(542) |
Likewise, the vector gravitational force exerted by object 1 on object 2 takes
the form
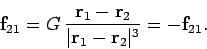 |
(543) |
The constant of proportionality, 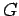 , appearing in the above formulae is called the
gravitational constant. Newton could only estimate the value of this quantity, which was first
directly measured by Henry Cavendish in 1798. The modern value of
, appearing in the above formulae is called the
gravitational constant. Newton could only estimate the value of this quantity, which was first
directly measured by Henry Cavendish in 1798. The modern value of 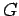 is
is
 |
(544) |
Note that the gravitational constant is numerically extremely small. This implies that gravity is
an intrinsically weak force. In fact, gravity usually only becomes significant if at least
one of the masses involved is of astronomical dimensions (e.g., it is a planet, or
a star).
Let us use Newton's law of gravity to account for the Earth's surface gravity.
Consider an object of mass  close to the surface of the Earth, whose mass
and radius are
close to the surface of the Earth, whose mass
and radius are
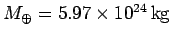 and
and
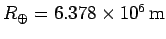 ,
respectively. Newton proved, after considerable effort, that the gravitational force
exerted by a spherical body (outside that body) is the same as that exerted by an
equivalent point mass located at the body's centre. Hence, the gravitational
force exerted by the Earth on the object in question is of magnitude
,
respectively. Newton proved, after considerable effort, that the gravitational force
exerted by a spherical body (outside that body) is the same as that exerted by an
equivalent point mass located at the body's centre. Hence, the gravitational
force exerted by the Earth on the object in question is of magnitude
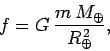 |
(545) |
and is directed towards the centre of the Earth. It follows that the equation of
motion of the object can be written
 |
(546) |
where 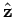 is a unit vector pointing straight upwards (i.e., away
from the Earth's centre). Canceling the factor
is a unit vector pointing straight upwards (i.e., away
from the Earth's centre). Canceling the factor  on either side of the above
equation, we obtain
on either side of the above
equation, we obtain
 |
(547) |
where
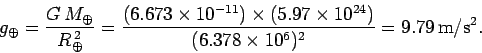 |
(548) |
Thus, we conclude that all objects on the Earth's surface, irrespective of
their mass, accelerate straight down (i.e., towards the Earth's centre)
with a constant acceleration of
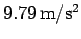 . This estimate for the
acceleration due to gravity is slightly off the conventional value of
. This estimate for the
acceleration due to gravity is slightly off the conventional value of
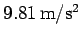 because the Earth is actually not quite spherical.
because the Earth is actually not quite spherical.
Since Newton's law of gravitation is universal, we immediately conclude that any
spherical body of mass  and radius
and radius  possesses a surface gravity
possesses a surface gravity 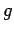 given
by the following formula:
given
by the following formula:
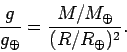 |
(549) |
Table 6 shows the surface gravity of various bodies in the Solar System,
estimated using the above expression. It can be seen that the surface gravity of the
Moon is only about one fifth of that of the Earth. No wonder Apollo astronauts were able
to jump so far on the Moon's surface! Prospective Mars colonists should note that they
will only weigh about a third of their terrestrial weight on Mars.
Table 6:
The mass,  , radius,
, radius,  , and surface gravity,
, and surface gravity, 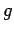 , of various
bodies in the Solar System. All quantities are expressed as fractions of the
corresponding terrestrial quantity.
, of various
bodies in the Solar System. All quantities are expressed as fractions of the
corresponding terrestrial quantity.
| Body |
 |
 |
 |
| Sun |
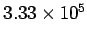 |
109.0 |
28.1 |
| Moon |
0.0123 |
0.273 |
0.17 |
| Mercury |
0.0553 |
0.383 |
0.38 |
| Venus |
0.816 |
0.949 |
0.91 |
| Earth |
1.000 |
1.000 |
1.000 |
| Mars |
0.108 |
0.533 |
0.38 |
| Jupiter |
318.3 |
11.21 |
2.5 |
| Saturn |
95.14 |
9.45 |
1.07 |
|



Next: Gravitational potential energy
Up: Orbital motion
Previous: Historical background
Richard Fitzpatrick
2006-02-02
![]() and
and ![]() , separated by a distance
, separated by a distance ![]() .
As illustrated in Fig. 104, the magnitude of the force of attraction
between these objects is
.
As illustrated in Fig. 104, the magnitude of the force of attraction
between these objects is
![]() and
and ![]() be the vector positions of the two objects,
respectively. The vector gravitational force exerted by object 2 on object 1 can
be written
be the vector positions of the two objects,
respectively. The vector gravitational force exerted by object 2 on object 1 can
be written
![]() , appearing in the above formulae is called the
gravitational constant. Newton could only estimate the value of this quantity, which was first
directly measured by Henry Cavendish in 1798. The modern value of
, appearing in the above formulae is called the
gravitational constant. Newton could only estimate the value of this quantity, which was first
directly measured by Henry Cavendish in 1798. The modern value of ![]() is
is
![]() close to the surface of the Earth, whose mass
and radius are
close to the surface of the Earth, whose mass
and radius are
![]() and
and
![]() ,
respectively. Newton proved, after considerable effort, that the gravitational force
exerted by a spherical body (outside that body) is the same as that exerted by an
equivalent point mass located at the body's centre. Hence, the gravitational
force exerted by the Earth on the object in question is of magnitude
,
respectively. Newton proved, after considerable effort, that the gravitational force
exerted by a spherical body (outside that body) is the same as that exerted by an
equivalent point mass located at the body's centre. Hence, the gravitational
force exerted by the Earth on the object in question is of magnitude
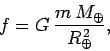

![]() and radius
and radius ![]() possesses a surface gravity
possesses a surface gravity ![]() given
by the following formula:
given
by the following formula: