


Next: The Planck radiation law
Up: Quantum statistics
Previous: Maxwell-Boltzmann statistics
The preceding analysis regarding the quantum statistics of ideal
gases is summarized in the following statements. The mean number of
particles occupying quantum state 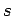 is given by
is given by
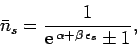 |
(617) |
where the upper sign corresponds to Fermi-Dirac statistics and the
lower sign corresponds to Bose-Einstein statistics. The parameter
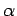 is determined via
is determined via
 |
(618) |
Finally, the partition function of the gas is given by
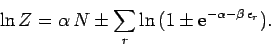 |
(619) |
Let us investigate the magnitude of 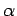 in some important limiting
cases. Consider, first of all, the case of a gas at a given temperature
when its concentration is made sufficiently low: i.e., when
in some important limiting
cases. Consider, first of all, the case of a gas at a given temperature
when its concentration is made sufficiently low: i.e., when
 is made sufficiently small. The relation (618) can only
be satisfied if each term in the sum over states is made
sufficiently small; i.e., if
is made sufficiently small. The relation (618) can only
be satisfied if each term in the sum over states is made
sufficiently small; i.e., if
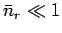 or
or
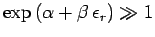 for all states
for all states 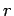 .
.
Consider, next, the case of a gas made up of a fixed number of particles
when its temperature is made sufficiently large: i.e., when 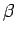 is
made sufficiently small. In the sum in Eq. (618), the terms of
appreciable magnitude are those for which
is
made sufficiently small. In the sum in Eq. (618), the terms of
appreciable magnitude are those for which
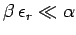 .
Thus, it follows that as
.
Thus, it follows that as
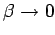 an increasing number of
terms with large values of
an increasing number of
terms with large values of 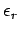 contribute substantially to this
sum. In order to prevent the sum from exceeding
contribute substantially to this
sum. In order to prevent the sum from exceeding  , the parameter
, the parameter 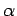 must become large enough that each term is made sufficiently small: i.e.,
it is again necessary that
must become large enough that each term is made sufficiently small: i.e.,
it is again necessary that
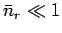 or
or
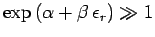 for all states
for all states 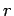 .
.
The above discussion suggests that if the concentration of an ideal
gas is made sufficiently low, or the temperature is made sufficiently high,
then 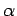 must become so large that
must become so large that
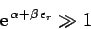 |
(620) |
for all 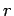 . Equivalently, this means that the number of particles occupying
each quantum state must
become so small that
. Equivalently, this means that the number of particles occupying
each quantum state must
become so small that
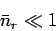 |
(621) |
for all 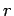 . It is conventional to refer to the limit of sufficiently
low concentration, or sufficiently high temperature, in which Eqs. (620)
and Eqs. (621) are satisfied, as the classical limit.
. It is conventional to refer to the limit of sufficiently
low concentration, or sufficiently high temperature, in which Eqs. (620)
and Eqs. (621) are satisfied, as the classical limit.
According to Eqs. (617) and (620), both
the Fermi-Dirac and Bose-Einstein
distributions reduce to
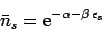 |
(622) |
in the classical limit, whereas the constraint (618) yields
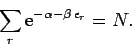 |
(623) |
The above expressions can be combined to give
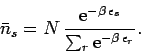 |
(624) |
It follows that in the classical limit of sufficiently low density,
or sufficiently high temperature, the quantum distribution functions,
whether Fermi-Dirac or Bose-Einstein, reduce to the Maxwell-Boltzmann
distribution. It is easily demonstrated that the physical criterion for the
validity of the classical approximation is that the mean separation between
particles should be much greater than their mean de Broglie wavelengths.
Let us now consider the behaviour of the partition function (619)
in the classical limit. We can expand the logarithm to
give
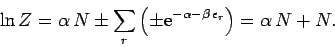 |
(625) |
However, according to Eq. (623),
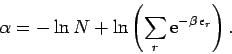 |
(626) |
It follows that
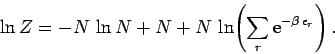 |
(627) |
Note that this does not equal the partition function 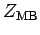 computed in Eq. (615) from Maxwell-Boltzmann statistics: i.e.,
computed in Eq. (615) from Maxwell-Boltzmann statistics: i.e.,
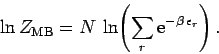 |
(628) |
In fact,
 |
(629) |
or
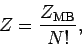 |
(630) |
where use has been made of Stirling's approximation (
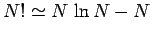 ),
since
),
since  is large. Here, the factor
is large. Here, the factor 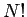 simply corresponds to the number
of different permutations of the
simply corresponds to the number
of different permutations of the  particles: permutations which are
physically meaningless when the particles are identical. Recall, that
we had to introduce precisely this factor, in an ad hoc fashion,
in Sect. 7.7 in order to avoid the non-physical consequences of
the Gibb's paradox. Clearly, there is no Gibb's paradox when an ideal
gas is treated properly via quantum mechanics.
particles: permutations which are
physically meaningless when the particles are identical. Recall, that
we had to introduce precisely this factor, in an ad hoc fashion,
in Sect. 7.7 in order to avoid the non-physical consequences of
the Gibb's paradox. Clearly, there is no Gibb's paradox when an ideal
gas is treated properly via quantum mechanics.
In the classical limit,
a full quantum mechanical analysis of an ideal gas reproduces the results
obtained in Sects. 7.6 and 7.7, except that the
arbitrary parameter 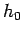 is replaced by Planck's constant
is replaced by Planck's constant
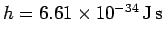 .
.
A gas in the classical limit, where the typical de Broglie wavelength of the
constituent particles is much smaller than the typical inter-particle
spacing, is said to be non-degenerate. In the opposite limit,
where the concentration and temperature are such that the typical
de Broglie wavelength
becomes comparable with the typical inter-particle spacing, and the actual
Fermi-Dirac or Bose-Einstein distributions must be employed, the
gas is said to be degenerate.



Next: The Planck radiation law
Up: Quantum statistics
Previous: Maxwell-Boltzmann statistics
Richard Fitzpatrick
2006-02-02
![]() in some important limiting
cases. Consider, first of all, the case of a gas at a given temperature
when its concentration is made sufficiently low: i.e., when
in some important limiting
cases. Consider, first of all, the case of a gas at a given temperature
when its concentration is made sufficiently low: i.e., when
![]() is made sufficiently small. The relation (618) can only
be satisfied if each term in the sum over states is made
sufficiently small; i.e., if
is made sufficiently small. The relation (618) can only
be satisfied if each term in the sum over states is made
sufficiently small; i.e., if
![]() or
or
![]() for all states
for all states ![]() .
.
![]() is
made sufficiently small. In the sum in Eq. (618), the terms of
appreciable magnitude are those for which
is
made sufficiently small. In the sum in Eq. (618), the terms of
appreciable magnitude are those for which
![]() .
Thus, it follows that as
.
Thus, it follows that as
![]() an increasing number of
terms with large values of
an increasing number of
terms with large values of ![]() contribute substantially to this
sum. In order to prevent the sum from exceeding
contribute substantially to this
sum. In order to prevent the sum from exceeding ![]() , the parameter
, the parameter ![]() must become large enough that each term is made sufficiently small: i.e.,
it is again necessary that
must become large enough that each term is made sufficiently small: i.e.,
it is again necessary that
![]() or
or
![]() for all states
for all states ![]() .
.
![]() must become so large that
must become so large that
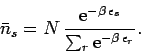
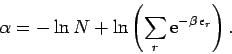
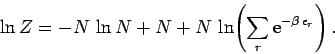
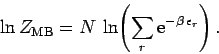
![]() is replaced by Planck's constant
is replaced by Planck's constant
![]() .
.