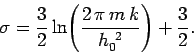

Next: Gibb's paradox
Up: Applications of statistical thermodynamics
Previous: Partition functions
Ideal monatomic gases
Let us now practice calculating thermodynamic relations using the partition
function by considering an example with which we are already quite familiar:
i.e.,
an ideal monatomic gas. Consider a gas consisting of  identical monatomic
molecules of mass
identical monatomic
molecules of mass 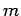 enclosed in a container of volume
enclosed in a container of volume 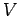 .
Let us denote the position and momentum
vectors of the
.
Let us denote the position and momentum
vectors of the 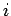 th molecule by
th molecule by 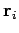 and
and
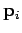 , respectively.
Since the gas is ideal, there are no interatomic forces, and the
total energy
is simply the sum of the individual kinetic energies of the molecules:
, respectively.
Since the gas is ideal, there are no interatomic forces, and the
total energy
is simply the sum of the individual kinetic energies of the molecules:
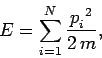 |
(427) |
where
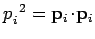 .
.
Let us treat the problem classically. In this approach, we divide up phase-space
into cells of equal volume 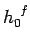 . Here,
. Here, 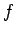 is the number of degrees of
freedom, and
is the number of degrees of
freedom, and 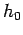 is a small constant with dimensions of angular momentum which
parameterizes the precision to which the positions and momenta of molecules
are determined (see Sect. 3.2).
Each cell in phase-space corresponds to a different state.
The partition function is the sum of the Boltzmann factor
is a small constant with dimensions of angular momentum which
parameterizes the precision to which the positions and momenta of molecules
are determined (see Sect. 3.2).
Each cell in phase-space corresponds to a different state.
The partition function is the sum of the Boltzmann factor
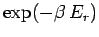 over all possible states, where
over all possible states, where 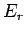 is the energy of state
is the energy of state 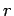 .
Classically, we can approximate the summation over cells in phase-space
as an integration over all phase-space. Thus,
.
Classically, we can approximate the summation over cells in phase-space
as an integration over all phase-space. Thus,
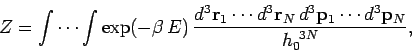 |
(428) |
where 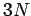 is the number of degrees of freedom of a monatomic gas containing
is the number of degrees of freedom of a monatomic gas containing
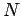 molecules. Making use of Eq. (427),
the above
expression reduces to
molecules. Making use of Eq. (427),
the above
expression reduces to
![\begin{displaymath}
Z = \frac{V^N}{h_0^{~3N}}\int\cdots \int \exp[-(\beta/2m)\,p...
...d^3{\bf p}_1
\cdots \exp[-(\beta/2m)\,p_N^{~2}]\,d^3{\bf p}_N.
\end{displaymath}](img1023.png) |
(429) |
Note that the integral over the coordinates of a given
molecule simply yields the volume
of the container, 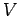 , since the energy
, since the energy 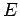 is independent of the
locations of the molecules
in an ideal gas. There are
is independent of the
locations of the molecules
in an ideal gas. There are 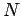 such integrals, so we obtain the factor
such integrals, so we obtain the factor
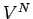 in the above expression. Note, also, that
each of the integrals over the molecular momenta in Eq. (429)
are identical: they differ only by irrelevant dummy variables of integration.
It follows that the partition function
in the above expression. Note, also, that
each of the integrals over the molecular momenta in Eq. (429)
are identical: they differ only by irrelevant dummy variables of integration.
It follows that the partition function 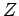 of the gas is made up of the product of
of the gas is made up of the product of
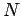 identical factors: i.e.,
identical factors: i.e.,
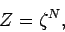 |
(430) |
where
![\begin{displaymath}
\zeta = \frac{V}{h_0^{~3}}\int \exp[-(\beta/2m)\,p^2]\,d^3{\bf p}
\end{displaymath}](img1025.png) |
(431) |
is the partition function for a single molecule. Of course, this
result is obvious, since we have already shown that the partition function for
a system made up of a number of weakly interacting subsystems is just the
product of the partition functions of the subsystems (see Sect. 7.5).
The integral in Eq. (431) is easily evaluated:
where use has been made of Eq. (79). Thus,
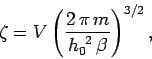 |
(433) |
and
![\begin{displaymath}
\ln Z = N\ln \zeta = N \left[\ln V - \frac{3}{2}\ln \beta +\frac{3}{2}
\ln\!\left(\frac{2\,\pi\, m}{h_0^{~2}}\right)\right].
\end{displaymath}](img1031.png) |
(434) |
The expression for the mean pressure (414) yields
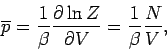 |
(435) |
which reduces to the ideal gas equation of state
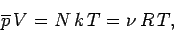 |
(436) |
where use has been made of
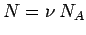 and
and 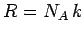 . According to Eq. (399), the mean
energy of the gas is given by
. According to Eq. (399), the mean
energy of the gas is given by
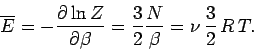 |
(437) |
Note that the internal
energy is a function of temperature alone, with no dependence on
volume. The molar heat capacity at constant volume of the gas is given by
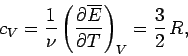 |
(438) |
so the mean energy can be written
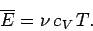 |
(439) |
We have seen all of the above results
before. Let us
now use the partition function to calculate a new result. The entropy of the
gas can be calculated quite simply from the expression
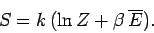 |
(440) |
Thus,
![\begin{displaymath}
S = \nu R \left[ \ln V -\frac{3}{2} \ln \beta + \frac{3}{2}\...
...eft(\frac{2\,\pi\, m }{h_0^{~2}}\right) + \frac{3}{2} \right],
\end{displaymath}](img1039.png) |
(441) |
or
![\begin{displaymath}
S = \nu R \left[ \ln V + \frac{3}{2}\ln T + \sigma\right],
\end{displaymath}](img1040.png) |
(442) |
where
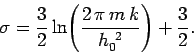 |
(443) |
The above expression for the entropy of an ideal gas is certainly new.
Unfortunately, it is also quite obviously incorrect!


Next: Gibb's paradox
Up: Applications of statistical thermodynamics
Previous: Partition functions
Richard Fitzpatrick
2006-02-02
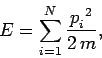
![]() . Here,
. Here, ![]() is the number of degrees of
freedom, and
is the number of degrees of
freedom, and ![]() is a small constant with dimensions of angular momentum which
parameterizes the precision to which the positions and momenta of molecules
are determined (see Sect. 3.2).
Each cell in phase-space corresponds to a different state.
The partition function is the sum of the Boltzmann factor
is a small constant with dimensions of angular momentum which
parameterizes the precision to which the positions and momenta of molecules
are determined (see Sect. 3.2).
Each cell in phase-space corresponds to a different state.
The partition function is the sum of the Boltzmann factor
![]() over all possible states, where
over all possible states, where ![]() is the energy of state
is the energy of state ![]() .
Classically, we can approximate the summation over cells in phase-space
as an integration over all phase-space. Thus,
.
Classically, we can approximate the summation over cells in phase-space
as an integration over all phase-space. Thus,
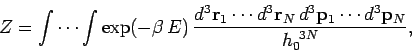
![$\displaystyle \int \exp[-(\beta/2m)\,p^2]\,d^3{\bf p}$](img1026.png)
![$\displaystyle \int_{-\infty}^{\infty}\exp[-(\beta/2m)\,p_x^{~2}]\,dp_x\,
\int_{-\infty}^{\infty}\exp[-(\beta/2m)\,p_y^{~2}]\,dp_y\,$](img1027.png)
![$\displaystyle \times \int_{-\infty}^{\infty}\exp[-(\beta/2m)\,p_z^{~2}]\,dp_z$](img1028.png)
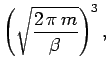
![\begin{displaymath}
\ln Z = N\ln \zeta = N \left[\ln V - \frac{3}{2}\ln \beta +\frac{3}{2}
\ln\!\left(\frac{2\,\pi\, m}{h_0^{~2}}\right)\right].
\end{displaymath}](img1031.png)
![\begin{displaymath}
S = \nu R \left[ \ln V -\frac{3}{2} \ln \beta + \frac{3}{2}\...
...eft(\frac{2\,\pi\, m }{h_0^{~2}}\right) + \frac{3}{2} \right],
\end{displaymath}](img1039.png)