


Next: The laws of thermodynamics
Up: Statistical thermodynamics
Previous: Uses of entropy
Entropy and quantum mechanics
The entropy of a system is defined in terms of the number
 of accessible microstates
consistent with an overall energy in the range
of accessible microstates
consistent with an overall energy in the range  to
to  via
via
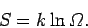 |
(249) |
We have already demonstrated that this definition is utterly insensitive to the
resolution 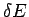 to which the macroscopic energy is measured
(see Sect. 5.7).
In classical mechanics, if a system possesses
to which the macroscopic energy is measured
(see Sect. 5.7).
In classical mechanics, if a system possesses 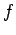 degrees of freedom then
phase-space is conventionally
subdivided into cells of arbitrarily chosen volume
degrees of freedom then
phase-space is conventionally
subdivided into cells of arbitrarily chosen volume 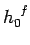 (see
Sect. 3.2). The number of accessible microstates is equivalent to the number
of these cells in the volume of phase-space consistent with an overall energy of
the system lying in the range
(see
Sect. 3.2). The number of accessible microstates is equivalent to the number
of these cells in the volume of phase-space consistent with an overall energy of
the system lying in the range  to
to  . Thus,
. Thus,
 |
(250) |
giving
 |
(251) |
Thus, in classical mechanics the entropy is undetermined to an arbitrary
additive constant which depends on the size of the cells in phase-space.
In fact, 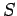 increases as the cell size decreases.
The second law of thermodynamics is only concerned with changes in entropy,
and is, therefore, unaffected by an additive constant. Likewise, macroscopic
thermodynamical quantities, such as the temperature and pressure, which can
be expressed as partial derivatives of the entropy with respect to various
macroscopic parameters [see Eqs. (242) and (243)] are unaffected by such a constant.
So, in classical mechanics the entropy is rather like a gravitational potential:
it is undetermined to an additive constant, but this does not affect any
physical laws.
increases as the cell size decreases.
The second law of thermodynamics is only concerned with changes in entropy,
and is, therefore, unaffected by an additive constant. Likewise, macroscopic
thermodynamical quantities, such as the temperature and pressure, which can
be expressed as partial derivatives of the entropy with respect to various
macroscopic parameters [see Eqs. (242) and (243)] are unaffected by such a constant.
So, in classical mechanics the entropy is rather like a gravitational potential:
it is undetermined to an additive constant, but this does not affect any
physical laws.
The non-unique value of the entropy comes about because
there is no limit to the precision to which the state of a classical system can be
specified. In other words, the cell size 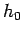 can be made arbitrarily small, which
corresponds to specifying the particle coordinates and momenta to arbitrary
accuracy. However, in quantum mechanics the uncertainty principle sets a
definite
limit to how accurately the particle coordinates and momenta can be specified.
In general,
can be made arbitrarily small, which
corresponds to specifying the particle coordinates and momenta to arbitrary
accuracy. However, in quantum mechanics the uncertainty principle sets a
definite
limit to how accurately the particle coordinates and momenta can be specified.
In general,
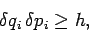 |
(252) |
where 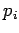 is the momentum conjugate to the generalized coordinate
is the momentum conjugate to the generalized coordinate 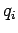 ,
and
,
and 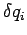 ,
, 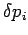 are the uncertainties in these quantities,
respectively. In fact, in quantum mechanics the number of accessible
quantum states
with the overall energy in the range
are the uncertainties in these quantities,
respectively. In fact, in quantum mechanics the number of accessible
quantum states
with the overall energy in the range  to
to  is completely determined.
This implies that, in reality, the entropy
of a system has a unique and unambiguous value. Quantum
mechanics can often be ``mocked up'' in classical mechanics by setting the
cell size in phase-space equal to Planck's constant, so that
is completely determined.
This implies that, in reality, the entropy
of a system has a unique and unambiguous value. Quantum
mechanics can often be ``mocked up'' in classical mechanics by setting the
cell size in phase-space equal to Planck's constant, so that 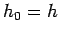 . This
automatically enforces the most restrictive form of the uncertainty principle,
. This
automatically enforces the most restrictive form of the uncertainty principle,
 . In many systems, the
substitution
. In many systems, the
substitution
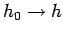 in Eq. (251) gives the same,
unique value for
in Eq. (251) gives the same,
unique value for 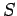 as
that obtained from a full quantum mechanical calculation.
as
that obtained from a full quantum mechanical calculation.
Consider a simple quantum mechanical system consisting of  non-interacting
spinless particles of mass
non-interacting
spinless particles of mass  confined in a cubic box of dimension
confined in a cubic box of dimension 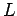 .
The energy levels of the
.
The energy levels of the 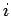 th particle are given by
th particle are given by
 |
(253) |
where 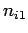 ,
, 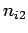 , and
, and 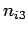 are three (positive) quantum numbers. The
overall energy of the system is the sum of the energies of the individual particles,
so that for a general state
are three (positive) quantum numbers. The
overall energy of the system is the sum of the energies of the individual particles,
so that for a general state 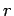
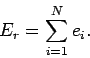 |
(254) |
The overall state of the system is completely
specified by 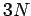 quantum numbers, so the number
of degrees of freedom is
quantum numbers, so the number
of degrees of freedom is 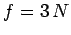 . The classical limit corresponds to the situation
where all of the quantum numbers are much greater than unity. In this limit, the
number of accessible states varies with energy according to our usual estimate
. The classical limit corresponds to the situation
where all of the quantum numbers are much greater than unity. In this limit, the
number of accessible states varies with energy according to our usual estimate
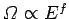 . The lowest possible energy state of the system, the
so-called ground-state, corresponds to the situation where all quantum numbers
take their lowest possible value, unity. Thus, the ground-state energy
. The lowest possible energy state of the system, the
so-called ground-state, corresponds to the situation where all quantum numbers
take their lowest possible value, unity. Thus, the ground-state energy 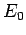 is
given by
is
given by
 |
(255) |
There is only one accessible microstate at the ground-state energy (i.e.,
that where all quantum numbers are unity), so by our usual definition of
entropy
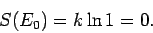 |
(256) |
In other words, there is no disorder in the system when all the particles are in their
ground-states.
Clearly, as the energy approaches the ground-state energy,
the number of accessible states becomes far less than
the usual classical estimate 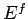 . This is true for all quantum mechanical systems.
In general, the number of microstates
varies roughly like
. This is true for all quantum mechanical systems.
In general, the number of microstates
varies roughly like
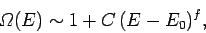 |
(257) |
where 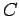 is a positive constant.
According to Eq. (187), the temperature varies approximately like
is a positive constant.
According to Eq. (187), the temperature varies approximately like
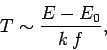 |
(258) |
provided
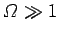 . Thus, as the absolute temperature of a system
approaches zero, the internal energy approaches a limiting value
. Thus, as the absolute temperature of a system
approaches zero, the internal energy approaches a limiting value 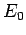 (the
quantum mechanical ground-state energy), and the entropy approaches the limiting
value zero.
This proposition is known as the third law of thermodynamics.
(the
quantum mechanical ground-state energy), and the entropy approaches the limiting
value zero.
This proposition is known as the third law of thermodynamics.
At low temperatures, great care must be taken to ensure that equilibrium
thermodynamical arguments are applicable, since the rate of attaining equilibrium may
be very slow. Another difficulty arises when dealing with a system in which the
atoms possess nuclear spins. Typically, when such a system is brought to a very
low temperature the entropy associated with the degrees of freedom not
involving nuclear spins becomes negligible. Nevertheless, the number of microstates
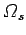 corresponding to the possible nuclear spin orientations may be very
large. Indeed, it may be just as large as the number of states at
room temperature. The reason for this is that nuclear magnetic moments are extremely small,
and, therefore, have extremely weak mutual interactions. Thus,
it only takes a tiny amount
of heat energy in the system to completely randomize the spin orientations.
Typically, a temperature as small as
corresponding to the possible nuclear spin orientations may be very
large. Indeed, it may be just as large as the number of states at
room temperature. The reason for this is that nuclear magnetic moments are extremely small,
and, therefore, have extremely weak mutual interactions. Thus,
it only takes a tiny amount
of heat energy in the system to completely randomize the spin orientations.
Typically, a temperature as small as 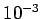 degrees kelvin above absolute zero
is sufficient to randomize the spins.
degrees kelvin above absolute zero
is sufficient to randomize the spins.
Suppose that the system consists of  atoms
of spin
atoms
of spin 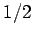 . Each spin can have two possible orientations. If there is enough
residual heat energy in the system to randomize the spins then each orientation
is equally likely. If follows that there are
. Each spin can have two possible orientations. If there is enough
residual heat energy in the system to randomize the spins then each orientation
is equally likely. If follows that there are
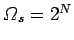 accessible spin
states. The entropy associated with these states is
accessible spin
states. The entropy associated with these states is
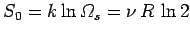 . Below some critical temperature,
. Below some critical temperature, 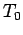 , the interaction between the
nuclear spins becomes significant, and the system settles down in
some unique quantum mechanical ground-state (e.g., with all spins aligned).
In this situation,
, the interaction between the
nuclear spins becomes significant, and the system settles down in
some unique quantum mechanical ground-state (e.g., with all spins aligned).
In this situation,
 ,
in accordance with the third law of thermodynamics. However, for temperatures
which are small, but not small enough to ``freeze out'' the nuclear spin degrees
of freedom, the entropy approaches a limiting value
,
in accordance with the third law of thermodynamics. However, for temperatures
which are small, but not small enough to ``freeze out'' the nuclear spin degrees
of freedom, the entropy approaches a limiting value 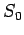 which depends only
on the kinds of atomic nuclei in the system. This limiting value is independent
of the spatial arrangement of the atoms, or the interactions between them.
Thus, for most practical purposes the third law of thermodynamics can be written
which depends only
on the kinds of atomic nuclei in the system. This limiting value is independent
of the spatial arrangement of the atoms, or the interactions between them.
Thus, for most practical purposes the third law of thermodynamics can be written
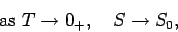 |
(259) |
where  denotes a temperature which is very close to absolute zero, but
still much larger than
denotes a temperature which is very close to absolute zero, but
still much larger than 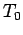 . This modification of the third law is
useful because it can be applied at temperatures which are not prohibitively low.
. This modification of the third law is
useful because it can be applied at temperatures which are not prohibitively low.



Next: The laws of thermodynamics
Up: Statistical thermodynamics
Previous: Uses of entropy
Richard Fitzpatrick
2006-02-02

![]() can be made arbitrarily small, which
corresponds to specifying the particle coordinates and momenta to arbitrary
accuracy. However, in quantum mechanics the uncertainty principle sets a
definite
limit to how accurately the particle coordinates and momenta can be specified.
In general,
can be made arbitrarily small, which
corresponds to specifying the particle coordinates and momenta to arbitrary
accuracy. However, in quantum mechanics the uncertainty principle sets a
definite
limit to how accurately the particle coordinates and momenta can be specified.
In general,
![]() non-interacting
spinless particles of mass
non-interacting
spinless particles of mass ![]() confined in a cubic box of dimension
confined in a cubic box of dimension ![]() .
The energy levels of the
.
The energy levels of the ![]() th particle are given by
th particle are given by
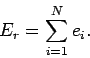
![]() . This is true for all quantum mechanical systems.
In general, the number of microstates
varies roughly like
. This is true for all quantum mechanical systems.
In general, the number of microstates
varies roughly like
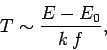
![]() corresponding to the possible nuclear spin orientations may be very
large. Indeed, it may be just as large as the number of states at
room temperature. The reason for this is that nuclear magnetic moments are extremely small,
and, therefore, have extremely weak mutual interactions. Thus,
it only takes a tiny amount
of heat energy in the system to completely randomize the spin orientations.
Typically, a temperature as small as
corresponding to the possible nuclear spin orientations may be very
large. Indeed, it may be just as large as the number of states at
room temperature. The reason for this is that nuclear magnetic moments are extremely small,
and, therefore, have extremely weak mutual interactions. Thus,
it only takes a tiny amount
of heat energy in the system to completely randomize the spin orientations.
Typically, a temperature as small as ![]() degrees kelvin above absolute zero
is sufficient to randomize the spins.
degrees kelvin above absolute zero
is sufficient to randomize the spins.
![]() atoms
of spin
atoms
of spin ![]() . Each spin can have two possible orientations. If there is enough
residual heat energy in the system to randomize the spins then each orientation
is equally likely. If follows that there are
. Each spin can have two possible orientations. If there is enough
residual heat energy in the system to randomize the spins then each orientation
is equally likely. If follows that there are
![]() accessible spin
states. The entropy associated with these states is
accessible spin
states. The entropy associated with these states is
![]() . Below some critical temperature,
. Below some critical temperature, ![]() , the interaction between the
nuclear spins becomes significant, and the system settles down in
some unique quantum mechanical ground-state (e.g., with all spins aligned).
In this situation,
, the interaction between the
nuclear spins becomes significant, and the system settles down in
some unique quantum mechanical ground-state (e.g., with all spins aligned).
In this situation,
![]() ,
in accordance with the third law of thermodynamics. However, for temperatures
which are small, but not small enough to ``freeze out'' the nuclear spin degrees
of freedom, the entropy approaches a limiting value
,
in accordance with the third law of thermodynamics. However, for temperatures
which are small, but not small enough to ``freeze out'' the nuclear spin degrees
of freedom, the entropy approaches a limiting value ![]() which depends only
on the kinds of atomic nuclei in the system. This limiting value is independent
of the spatial arrangement of the atoms, or the interactions between them.
Thus, for most practical purposes the third law of thermodynamics can be written
which depends only
on the kinds of atomic nuclei in the system. This limiting value is independent
of the spatial arrangement of the atoms, or the interactions between them.
Thus, for most practical purposes the third law of thermodynamics can be written