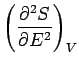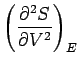

Next: Entropy and quantum mechanics
Up: Statistical thermodynamics
Previous: Properties of entropy
Uses of entropy
We have defined a new function called entropy, denoted 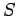 ,
which parameterizes the amount of disorder in a macroscopic
system. The entropy of an equilibrium
macrostate
is related to the number of accessible microstates
,
which parameterizes the amount of disorder in a macroscopic
system. The entropy of an equilibrium
macrostate
is related to the number of accessible microstates 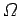 via
via
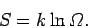 |
(235) |
On a macroscopic level, the increase in entropy due to a quasi-static change
in which an infinitesimal amount of heat
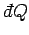 is absorbed by the system is
given by
is absorbed by the system is
given by
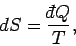 |
(236) |
where 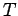 is the absolute temperature of the system.
The second law of thermodynamics states that the entropy of an isolated system
can never spontaneously decrease. Let us now briefly examine some consequences
of these results.
is the absolute temperature of the system.
The second law of thermodynamics states that the entropy of an isolated system
can never spontaneously decrease. Let us now briefly examine some consequences
of these results.
Consider two bodies, 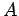 and
and 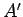 ,
which are in thermal contact but can do no work
on one another. We know what is supposed to happen here. Heat flows from the
hotter to the colder of the two bodies until their temperatures are the same.
Consider a quasi-static exchange of heat between the two bodies. According to the
first law of thermodynamics, if an infinitesimal amount of heat
,
which are in thermal contact but can do no work
on one another. We know what is supposed to happen here. Heat flows from the
hotter to the colder of the two bodies until their temperatures are the same.
Consider a quasi-static exchange of heat between the two bodies. According to the
first law of thermodynamics, if an infinitesimal amount of heat
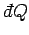 is
absorbed by
is
absorbed by 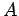 then infinitesimal heat
then infinitesimal heat
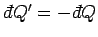 is absorbed
by
is absorbed
by 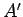 . The increase in the entropy of system
. The increase in the entropy of system 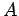 is
is
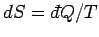 and
the corresponding increase in the entropy
of
and
the corresponding increase in the entropy
of 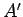 is
is
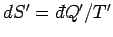 . Here,
. Here, 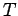 and
and 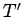 are the temperatures of the two
systems, respectively. Note that
are the temperatures of the two
systems, respectively. Note that
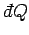 is assumed to the sufficiently small
that the heat transfer does not substantially
modify the temperatures of either system. The change in entropy of the whole
system is
is assumed to the sufficiently small
that the heat transfer does not substantially
modify the temperatures of either system. The change in entropy of the whole
system is
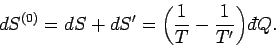 |
(237) |
This change must be positive or zero,
according to the second law of thermodynamics, so
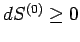 . It follows that
. It follows that
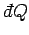 is positive (i.e., heat flows from
is positive (i.e., heat flows from
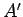 to
to 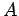 ) when
) when 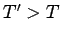 , and vice versa. The
spontaneous flow of heat only ceases when
, and vice versa. The
spontaneous flow of heat only ceases when 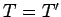 . Thus, the direction of
spontaneous heat flow is a consequence of the second law of thermodynamics.
Note that the spontaneous flow of heat between bodies at different temperatures
is always an irreversible process which
increases the entropy, or disorder, of the
Universe.
. Thus, the direction of
spontaneous heat flow is a consequence of the second law of thermodynamics.
Note that the spontaneous flow of heat between bodies at different temperatures
is always an irreversible process which
increases the entropy, or disorder, of the
Universe.
Consider, now, the slightly more complicated situation in which the two systems can
exchange heat and also do work on one another via a movable partition.
Suppose that the total volume is invariant, so that
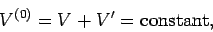 |
(238) |
where 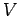 and
and 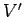 are the volumes of
are the volumes of 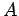 and
and 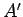 , respectively.
Consider a
quasi-static change in which system
, respectively.
Consider a
quasi-static change in which system 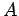 absorbs an infinitesimal
amount of heat
absorbs an infinitesimal
amount of heat
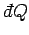 and its volume simultaneously increases by an infinitesimal amount
and its volume simultaneously increases by an infinitesimal amount
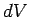 . The infinitesimal
amount of work done by system
. The infinitesimal
amount of work done by system 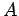 is
is
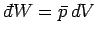 (see Sect. 4.4), where
(see Sect. 4.4), where 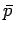 is the mean pressure of
is the mean pressure of 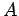 .
According to the first law of thermodynamics,
.
According to the first law of thermodynamics,
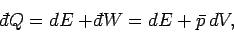 |
(239) |
where 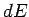 is the change in the internal energy of
is the change in the internal energy of 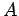 . Since
. Since
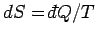 ,
the increase in entropy of system
,
the increase in entropy of system 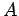 is written
is written
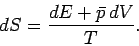 |
(240) |
Likewise, the increase in entropy of system 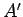 is given by
is given by
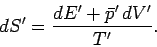 |
(241) |
According to Eq. (240),
where the subscripts are to remind us what is
held constant in the partial derivatives.
We can write a similar pair of equations for the system 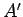 .
.
The overall system is assumed to be isolated, so conservation of energy
gives 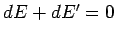 . Furthermore, Eq. (238) implies that
. Furthermore, Eq. (238) implies that
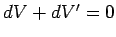 . It follows that the total change in entropy is given by
. It follows that the total change in entropy is given by
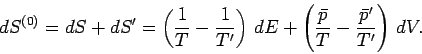 |
(244) |
The equilibrium state is the most probable state (see Sect. 5.2).
According to statistical
mechanics, this is equivalent to the state with the largest number of accessible
microstates. Finally, Eq. (235) implies that this is the
maximum entropy state. The system can never spontaneously leave a
maximum entropy state,
since this would imply a spontaneous reduction in
entropy, which is forbidden by the second law of thermodynamics.
A maximum or minimum
entropy state must
satisfy 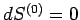 for arbitrary small variations of the energy
and external parameters.
It follows from Eq. (244) that
for arbitrary small variations of the energy
and external parameters.
It follows from Eq. (244) that
for such a state. This corresponds to a maximum entropy state (i.e.,
an equilibrium state) provided
with a similar pair of inequalities for system 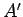 . The usual estimate
. The usual estimate
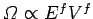 , giving
, giving
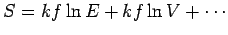 , ensures that the above inequalities
are satisfied in conventional macroscopic systems. In the maximum entropy state
the systems
, ensures that the above inequalities
are satisfied in conventional macroscopic systems. In the maximum entropy state
the systems 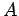 and
and 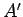 have equal temperatures (i.e., they are in thermal
equilibrium) and equal pressures (i.e., they are in mechanical equilibrium).
The second law of thermodynamics implies that the two interacting systems will
evolve towards this state, and will
then remain in it
indefinitely (if left undisturbed).
have equal temperatures (i.e., they are in thermal
equilibrium) and equal pressures (i.e., they are in mechanical equilibrium).
The second law of thermodynamics implies that the two interacting systems will
evolve towards this state, and will
then remain in it
indefinitely (if left undisturbed).


Next: Entropy and quantum mechanics
Up: Statistical thermodynamics
Previous: Properties of entropy
Richard Fitzpatrick
2006-02-02
![]() and
and ![]() ,
which are in thermal contact but can do no work
on one another. We know what is supposed to happen here. Heat flows from the
hotter to the colder of the two bodies until their temperatures are the same.
Consider a quasi-static exchange of heat between the two bodies. According to the
first law of thermodynamics, if an infinitesimal amount of heat
,
which are in thermal contact but can do no work
on one another. We know what is supposed to happen here. Heat flows from the
hotter to the colder of the two bodies until their temperatures are the same.
Consider a quasi-static exchange of heat between the two bodies. According to the
first law of thermodynamics, if an infinitesimal amount of heat
![]() is
absorbed by
is
absorbed by ![]() then infinitesimal heat
then infinitesimal heat
![]() is absorbed
by
is absorbed
by ![]() . The increase in the entropy of system
. The increase in the entropy of system ![]() is
is
![]() and
the corresponding increase in the entropy
of
and
the corresponding increase in the entropy
of ![]() is
is
![]() . Here,
. Here, ![]() and
and ![]() are the temperatures of the two
systems, respectively. Note that
are the temperatures of the two
systems, respectively. Note that
![]() is assumed to the sufficiently small
that the heat transfer does not substantially
modify the temperatures of either system. The change in entropy of the whole
system is
is assumed to the sufficiently small
that the heat transfer does not substantially
modify the temperatures of either system. The change in entropy of the whole
system is
![]() . Furthermore, Eq. (238) implies that
. Furthermore, Eq. (238) implies that
![]() . It follows that the total change in entropy is given by
. It follows that the total change in entropy is given by