


Next: Mechanical interaction between macrosystems
Up: Statistical thermodynamics
Previous: Thermal interaction between macrosystems
Temperature
Suppose that the systems  and
and 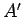 are initially thermally isolated from one
another, with respective energies
are initially thermally isolated from one
another, with respective energies 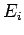 and
and 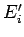 .
(Since the energy of an isolated system cannot fluctuate, we do not have to
bother with mean energies here.) If the two systems are
subsequently placed in thermal contact, so that they are
free to exchange heat energy, then,
in general, the resulting state is an extremely improbable one
[i.e.,
.
(Since the energy of an isolated system cannot fluctuate, we do not have to
bother with mean energies here.) If the two systems are
subsequently placed in thermal contact, so that they are
free to exchange heat energy, then,
in general, the resulting state is an extremely improbable one
[i.e., 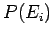 is much less than the peak probability]. The configuration will,
therefore,
tend to change in time until the two systems attain final mean energies
is much less than the peak probability]. The configuration will,
therefore,
tend to change in time until the two systems attain final mean energies 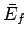 and
and 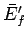 which are such that
which are such that
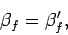 |
(176) |
where
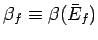 and
and
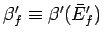 . This
corresponds to the state of maximum probability (see Sect. 5.2).
In the special case where the initial energies,
. This
corresponds to the state of maximum probability (see Sect. 5.2).
In the special case where the initial energies, 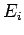 and
and 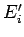 , lie very close to
the final mean energies,
, lie very close to
the final mean energies, 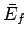 and
and 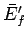 , respectively, there is no
change in the two systems when they are brought into thermal contact, since the
initial state already corresponds to a state of maximum probability.
, respectively, there is no
change in the two systems when they are brought into thermal contact, since the
initial state already corresponds to a state of maximum probability.
It follows from energy conservation that
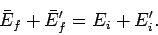 |
(177) |
The mean energy change in each system is simply the net heat absorbed, so that
The conservation of energy then reduces to
 |
(180) |
i.e., the heat given off by one system is equal to the heat absorbed by the other
(in our notation absorbed
heat is positive and emitted heat is negative).
It is clear that if the systems  and
and 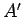 are suddenly
brought into thermal contact then they will only exchange heat and evolve towards a
new equilibrium state if the final state is
more probable than the initial one. In other words, if
are suddenly
brought into thermal contact then they will only exchange heat and evolve towards a
new equilibrium state if the final state is
more probable than the initial one. In other words, if
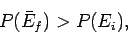 |
(181) |
or
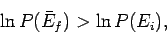 |
(182) |
since the logarithm is a monotonic function. The above inequality can be written
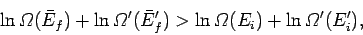 |
(183) |
with the aid of Eq. (159). Taylor expansion to first order yields
 |
(184) |
which finally gives
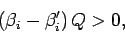 |
(185) |
where
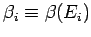 ,
,
 ,
and use has been made of Eq. (180).
,
and use has been made of Eq. (180).
It is clear, from the above, that the parameter 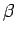 , defined
, defined
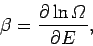 |
(186) |
has the following properties:
- If two systems separately in equilibrium have the same value of
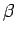 then
the systems will remain in equilibrium when brought into thermal contact with
one another.
then
the systems will remain in equilibrium when brought into thermal contact with
one another.
- If two systems separately in equilibrium have different values of
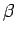 then the systems will not remain
in equilibrium when brought into thermal contact with
one another. Instead, the system with the higher value of
then the systems will not remain
in equilibrium when brought into thermal contact with
one another. Instead, the system with the higher value of 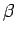 will absorb heat from the other system until the two
will absorb heat from the other system until the two 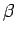 values are
the same [see Eq. (185)].
values are
the same [see Eq. (185)].
Incidentally, a partial derivative is used in Eq. (186)
because in a purely thermal interaction the external parameters of the
system are held constant whilst the energy changes.
Let us define the dimensionless parameter  , such that
, such that
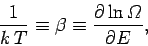 |
(187) |
where 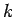 is a positive constant having the dimensions of energy. The parameter
is a positive constant having the dimensions of energy. The parameter  is termed the thermodynamic temperature, and controls heat flow in much the
same manner as a conventional temperature. Thus, if two isolated systems in
equilibrium possess the same thermodynamic temperature then they will remain in equilibrium
when brought into thermal contact. However,
if the two systems have different thermodynamic temperatures
then heat will flow from the system with the higher temperature
(i.e., the ``hotter''
system) to the system with the lower temperature until the temperatures of the
two systems are the same. In addition, suppose that we have three systems
is termed the thermodynamic temperature, and controls heat flow in much the
same manner as a conventional temperature. Thus, if two isolated systems in
equilibrium possess the same thermodynamic temperature then they will remain in equilibrium
when brought into thermal contact. However,
if the two systems have different thermodynamic temperatures
then heat will flow from the system with the higher temperature
(i.e., the ``hotter''
system) to the system with the lower temperature until the temperatures of the
two systems are the same. In addition, suppose that we have three systems  ,
, 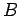 ,
and
,
and 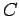 . We know that if
. We know that if  and
and 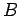 remain in equilibrium when brought into thermal
contact then their temperatures are the same, so that
remain in equilibrium when brought into thermal
contact then their temperatures are the same, so that 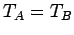 . Similarly, if
. Similarly, if
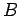 and
and 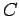 remain in equilibrium when brought into thermal contact, then
remain in equilibrium when brought into thermal contact, then
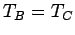 . But, we can then conclude that
. But, we can then conclude that 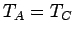 , so systems
, so systems  and
and 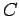 will also remain in equilibrium when brought into thermal contact. Thus, we arrive at
the following statement, which is sometimes called the zeroth law of
thermodynamics:
will also remain in equilibrium when brought into thermal contact. Thus, we arrive at
the following statement, which is sometimes called the zeroth law of
thermodynamics:
If two systems are separately in thermal equilibrium with a third system
then they must also be
in thermal equilibrium with one another.
The thermodynamic temperature of a macroscopic body, as defined in Eq. (187),
depends
only on the rate of change of
the number of accessible microstates with the total energy. Thus, it is possible
to define a thermodynamic
temperature for systems with radically different microscopic
structures (e.g., matter and radiation).
The thermodynamic, or absolute, scale of temperature is measured in
degrees kelvin.
The parameter 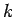 is chosen to make this temperature scale
accord as much as possible
with more conventional temperature scales. The choice
is chosen to make this temperature scale
accord as much as possible
with more conventional temperature scales. The choice
 |
(188) |
ensures that there are 100 degrees kelvin between the freezing and boiling points
of water at atmospheric pressure (the two temperatures are
273.15 and 373.15 degrees kelvin, respectively).
The above number is known as the Boltzmann
constant. In fact, the Boltzmann constant is fixed by international
convention so as to make the triple point of water (i.e., the unique
temperature at which the three phases of water co-exist in thermal equilibrium)
exactly
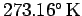 . Note that the zero of the thermodynamic scale, the
so called absolute zero of temperature, does not correspond to the freezing
point of water, but to some far more physically significant temperature which we
shall discuss presently.
. Note that the zero of the thermodynamic scale, the
so called absolute zero of temperature, does not correspond to the freezing
point of water, but to some far more physically significant temperature which we
shall discuss presently.
The familiar
 scaling for translational degrees of freedom yields
scaling for translational degrees of freedom yields
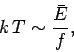 |
(189) |
using Eq. (187),
so 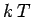 is a rough measure of the mean energy associated with
each degree of freedom in the system. In fact, for a classical system (i.e.,
one in which
quantum effects are unimportant) it is possible to show that the mean energy
associated with each degree of freedom is
exactly
is a rough measure of the mean energy associated with
each degree of freedom in the system. In fact, for a classical system (i.e.,
one in which
quantum effects are unimportant) it is possible to show that the mean energy
associated with each degree of freedom is
exactly  . This result, which is known as the
equipartition theorem, will be discussed
in
more detail later
on in this course.
. This result, which is known as the
equipartition theorem, will be discussed
in
more detail later
on in this course.
The absolute
temperature  is usually positive,
since
is usually positive,
since
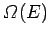 is ordinarily a very rapidly increasing function of
energy.
In fact, this is the case for all conventional systems
where the kinetic energy of the particles is taken into account, because there is
no upper bound on the possible energy of the system,
and
is ordinarily a very rapidly increasing function of
energy.
In fact, this is the case for all conventional systems
where the kinetic energy of the particles is taken into account, because there is
no upper bound on the possible energy of the system,
and
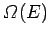 consequently increases
roughly like
consequently increases
roughly like 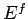 . It is, however, possible to envisage a situation in which we
ignore the translational degrees of freedom of a system, and concentrate only
on its spin degrees of freedom. In this case, there is an upper bound to
the possible energy of the system (i.e., all spins lined up anti-parallel to
an applied magnetic field). Consequently, the total number of states available to
the system is finite. In this situation, the density of spin states
. It is, however, possible to envisage a situation in which we
ignore the translational degrees of freedom of a system, and concentrate only
on its spin degrees of freedom. In this case, there is an upper bound to
the possible energy of the system (i.e., all spins lined up anti-parallel to
an applied magnetic field). Consequently, the total number of states available to
the system is finite. In this situation, the density of spin states
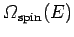 first increases with increasing energy, as in conventional
systems, but then reaches a maximum and decreases again. Thus, it is possible to
get absolute spin temperatures which are negative, as well as positive.
first increases with increasing energy, as in conventional
systems, but then reaches a maximum and decreases again. Thus, it is possible to
get absolute spin temperatures which are negative, as well as positive.
In Lavoisier's calorific theory, the basic mechanism which forces heat
to flow from hot to cold bodies is the supposed mutual repulsion of the constituent
particles of calorific fluid. In statistical mechanics,
the explanation is far less contrived. Heat flow occurs
because statistical systems tend to evolve towards their most
probable states, subject to the imposed physical constraints.
When two bodies at different temperatures are suddenly
placed in thermal contact, the initial state
corresponds to a spectacularly improbable state of the overall system. For systems
containing of order 1 mole of particles, the only reasonably probable final
equilibrium
states are such that the two bodies differ in temperature by less than 1 part in 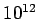 .
The evolution of the system towards these final states
(i.e., towards thermal equilibrium) is effectively driven by
probability.
.
The evolution of the system towards these final states
(i.e., towards thermal equilibrium) is effectively driven by
probability.



Next: Mechanical interaction between macrosystems
Up: Statistical thermodynamics
Previous: Thermal interaction between macrosystems
Richard Fitzpatrick
2006-02-02
![]() and
and ![]() are suddenly
brought into thermal contact then they will only exchange heat and evolve towards a
new equilibrium state if the final state is
more probable than the initial one. In other words, if
are suddenly
brought into thermal contact then they will only exchange heat and evolve towards a
new equilibrium state if the final state is
more probable than the initial one. In other words, if
![]() , defined
, defined
![]() , such that
, such that
![]() is chosen to make this temperature scale
accord as much as possible
with more conventional temperature scales. The choice
is chosen to make this temperature scale
accord as much as possible
with more conventional temperature scales. The choice
![]() scaling for translational degrees of freedom yields
scaling for translational degrees of freedom yields
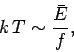
![]() is usually positive,
since
is usually positive,
since
![]() is ordinarily a very rapidly increasing function of
energy.
In fact, this is the case for all conventional systems
where the kinetic energy of the particles is taken into account, because there is
no upper bound on the possible energy of the system,
and
is ordinarily a very rapidly increasing function of
energy.
In fact, this is the case for all conventional systems
where the kinetic energy of the particles is taken into account, because there is
no upper bound on the possible energy of the system,
and
![]() consequently increases
roughly like
consequently increases
roughly like ![]() . It is, however, possible to envisage a situation in which we
ignore the translational degrees of freedom of a system, and concentrate only
on its spin degrees of freedom. In this case, there is an upper bound to
the possible energy of the system (i.e., all spins lined up anti-parallel to
an applied magnetic field). Consequently, the total number of states available to
the system is finite. In this situation, the density of spin states
. It is, however, possible to envisage a situation in which we
ignore the translational degrees of freedom of a system, and concentrate only
on its spin degrees of freedom. In this case, there is an upper bound to
the possible energy of the system (i.e., all spins lined up anti-parallel to
an applied magnetic field). Consequently, the total number of states available to
the system is finite. In this situation, the density of spin states
![]() first increases with increasing energy, as in conventional
systems, but then reaches a maximum and decreases again. Thus, it is possible to
get absolute spin temperatures which are negative, as well as positive.
first increases with increasing energy, as in conventional
systems, but then reaches a maximum and decreases again. Thus, it is possible to
get absolute spin temperatures which are negative, as well as positive.
![]() .
The evolution of the system towards these final states
(i.e., towards thermal equilibrium) is effectively driven by
probability.
.
The evolution of the system towards these final states
(i.e., towards thermal equilibrium) is effectively driven by
probability.