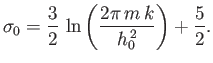Next: General Paramagnetism
Up: Applications of Statistical Thermodynamics
Previous: Ideal Monatomic Gas
Gibb's Paradox
First of all, let us be clear why Equation (7.78) is
incorrect.
We can see that
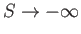 as
as
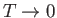 , which contradicts
the
third law of thermodynamics. However,
this is not a problem. Equation (7.78) was derived
using classical physics, which breaks down at low temperatures. Thus, we would
not expect this equation to give a sensible answer close to the absolute zero of temperature.
, which contradicts
the
third law of thermodynamics. However,
this is not a problem. Equation (7.78) was derived
using classical physics, which breaks down at low temperatures. Thus, we would
not expect this equation to give a sensible answer close to the absolute zero of temperature.
Equation (7.78) is wrong because it implies that the entropy does not behave
properly as an extensive quantity. Thermodynamic quantities can be
divided into two groups; extensive and intensive.
Extensive quantities increase
by a factor 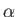 when the size of the system under consideration is
increased by the same factor. Intensive quantities stay the same. Energy and volume
are typical extensive quantities. Pressure and temperature are typical intensive
quantities. Entropy is very definitely an extensive quantity. We have previously shown
that the entropies of two weakly-interacting systems
are additive. [See Equation (7.62).] Thus, if we double the size of a system then we expect the
entropy to double as well. Suppose that we have a system of
volume
when the size of the system under consideration is
increased by the same factor. Intensive quantities stay the same. Energy and volume
are typical extensive quantities. Pressure and temperature are typical intensive
quantities. Entropy is very definitely an extensive quantity. We have previously shown
that the entropies of two weakly-interacting systems
are additive. [See Equation (7.62).] Thus, if we double the size of a system then we expect the
entropy to double as well. Suppose that we have a system of
volume  , containing
, containing 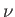 moles of ideal gas at temperature
moles of ideal gas at temperature  . Doubling
the size of the system is like joining two identical systems together to
form a new system of volume
. Doubling
the size of the system is like joining two identical systems together to
form a new system of volume 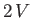 , containing
, containing 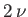 moles of gas at temperature
moles of gas at temperature  .
Let
.
Let
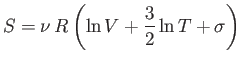 |
(7.80) |
denote the entropy of the original system, and let
![$\displaystyle S' = 2 \nu R \left[\ln (2 V) + \frac{3}{2} \ln T + \sigma\right]$](img1413.png) |
(7.81) |
denote the entropy of the double-sized system. Clearly, if entropy is an extensive
quantity then we should have
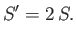 |
(7.82) |
But, in fact, we find that
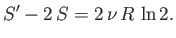 |
(7.83) |
So, the entropy of the double-sized system is more than double the entropy of the
original system.
Where does this extra entropy come from? Let us consider a little more carefully
how we might go about doubling the size of our system. Suppose that we put
another identical system adjacent to it, and separate the two
systems by a partition.
Let us now suddenly remove the partition. If entropy is
a properly extensive quantity then the entropy of the overall system
should be the same before and after the partition is removed. It is certainly the
case that the energy (another extensive quantity) of the overall system stays the
same. However, according to Equation (7.83), the overall entropy of the system
increases by
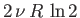 after the partition is removed. Suppose, now, that the second system
is identical to the first system in all
respects, except that its molecules are in some way slightly
different to the molecules in the first system, so that the two sets of
molecules are distinguishable.
In this case, we would certainly expect an overall
increase in
entropy when the partition is removed. Before the partition is removed,
it separates type 1 molecules from type 2 molecules.
After the partition is removed, molecules of both
types become jumbled together. This is clearly an
irreversible process. We cannot imagine the molecules spontaneously sorting
themselves out again. The increase in entropy associated with this jumbling is
called entropy of mixing, and is easily calculated. We know that the number
of accessible states of an ideal gas varies with volume like
after the partition is removed. Suppose, now, that the second system
is identical to the first system in all
respects, except that its molecules are in some way slightly
different to the molecules in the first system, so that the two sets of
molecules are distinguishable.
In this case, we would certainly expect an overall
increase in
entropy when the partition is removed. Before the partition is removed,
it separates type 1 molecules from type 2 molecules.
After the partition is removed, molecules of both
types become jumbled together. This is clearly an
irreversible process. We cannot imagine the molecules spontaneously sorting
themselves out again. The increase in entropy associated with this jumbling is
called entropy of mixing, and is easily calculated. We know that the number
of accessible states of an ideal gas varies with volume like
 . The volume accessible to type 1 molecules clearly doubles after the
partition is removed, as does the volume accessible to type 2 molecules.
Using the fundamental formula
. The volume accessible to type 1 molecules clearly doubles after the
partition is removed, as does the volume accessible to type 2 molecules.
Using the fundamental formula
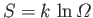 , the increase in entropy
due to mixing is given by
, the increase in entropy
due to mixing is given by
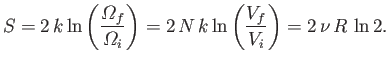 |
(7.84) |
It is clear that the additional entropy,
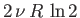 ,
that appears when we
double the size of an ideal gas
system, by joining together two identical systems,
is entropy of mixing of the molecules contained in the original systems.
But, if the
molecules in these two systems are indistinguishable then why should there be any
entropy of mixing? Obviously, there is no entropy of mixing in this case.
At this point, we can begin to understand what has gone wrong in our calculation.
We have calculated the partition function assuming
that all of the molecules in our system have the
same mass and temperature, but we have not explicitly taken into account
the fact that we consider the molecules to be indistinguishable.
In other words, we have been treating the molecules in our ideal gas as if each
carried a little license plate, or a social security number, so that we could always
tell one from another. In quantum mechanics,
which is what we really should be using to study microscopic phenomena, the
essential indistinguishability of atoms and molecules is hard-wired into the
theory at a very low level. Our problem is that we have been taking the classical
approach a little too seriously. It is plainly nonsense to pretend that we can
distinguish molecules in a statistical problem where we cannot closely
follow the motions
of individual particles. A paradox arises if we try to treat molecules
as if they were distinguishable. This is called Gibb's paradox, after
the American physicist Josiah Gibbs, who first discussed it. The resolution
of Gibb's paradox is quite simple: treat all molecules of the same species
as if they were indistinguishable.
,
that appears when we
double the size of an ideal gas
system, by joining together two identical systems,
is entropy of mixing of the molecules contained in the original systems.
But, if the
molecules in these two systems are indistinguishable then why should there be any
entropy of mixing? Obviously, there is no entropy of mixing in this case.
At this point, we can begin to understand what has gone wrong in our calculation.
We have calculated the partition function assuming
that all of the molecules in our system have the
same mass and temperature, but we have not explicitly taken into account
the fact that we consider the molecules to be indistinguishable.
In other words, we have been treating the molecules in our ideal gas as if each
carried a little license plate, or a social security number, so that we could always
tell one from another. In quantum mechanics,
which is what we really should be using to study microscopic phenomena, the
essential indistinguishability of atoms and molecules is hard-wired into the
theory at a very low level. Our problem is that we have been taking the classical
approach a little too seriously. It is plainly nonsense to pretend that we can
distinguish molecules in a statistical problem where we cannot closely
follow the motions
of individual particles. A paradox arises if we try to treat molecules
as if they were distinguishable. This is called Gibb's paradox, after
the American physicist Josiah Gibbs, who first discussed it. The resolution
of Gibb's paradox is quite simple: treat all molecules of the same species
as if they were indistinguishable.
In our previous calculation of the ideal gas partition function,
we inadvertently treated
each of the  molecules in the gas as distinguishable. Because of this,
we over-counted the
number of states of the system. Because the
molecules in the gas as distinguishable. Because of this,
we over-counted the
number of states of the system. Because the 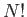 possible permutations of the
molecules amongst themselves do not lead to physically different situations,
and, therefore, cannot be counted as separate states, the number of actual states of
the system is a factor
possible permutations of the
molecules amongst themselves do not lead to physically different situations,
and, therefore, cannot be counted as separate states, the number of actual states of
the system is a factor 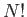 less than what we initially thought. We can
easily correct our partition function by simply dividing by this factor, so that
less than what we initially thought. We can
easily correct our partition function by simply dividing by this factor, so that
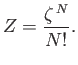 |
(7.85) |
This gives
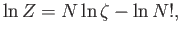 |
(7.86) |
or
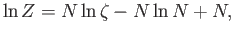 |
(7.87) |
using Stirling's approximation. Note that our new version of 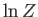 differs from our previous version by an additive term involving the number of
particles in the system. This explains why our calculations of the mean pressure
and mean energy, which depend on partial derivatives of
differs from our previous version by an additive term involving the number of
particles in the system. This explains why our calculations of the mean pressure
and mean energy, which depend on partial derivatives of 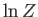 with respect to
the volume and the temperature parameter
with respect to
the volume and the temperature parameter 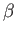 , respectively,
came out all right. However,
our expression for the entropy
, respectively,
came out all right. However,
our expression for the entropy 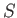 is modified by this additive term. The new
expression is
is modified by this additive term. The new
expression is
![$\displaystyle S = \nu R\left[ \ln V - \frac{3}{2} \ln \beta +\frac{3}{2} \ln\left(\frac{2\pi m k}{h_0^{ 2}}\right) + \frac{3}{2}\right]+ k (-N\ln N + N).$](img1424.png) |
(7.88) |
This gives
![$\displaystyle S = \nu R \left[ \ln\left( \frac{V}{N}\right) + \frac{3}{2} \ln T + \sigma_0\right]$](img1425.png) |
(7.89) |
where
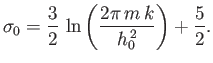 |
(7.90) |
It is clear that the entropy behaves properly as
an extensive quantity in Equation (7.89). In other words, it increases by a factor 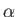 when
when 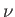 ,
,  ,
and
,
and  each increase by the same factor.
each increase by the same factor.



Next: General Paramagnetism
Up: Applications of Statistical Thermodynamics
Previous: Ideal Monatomic Gas
Richard Fitzpatrick
2016-01-25
![]() as
as
![]() , which contradicts
the
third law of thermodynamics. However,
this is not a problem. Equation (7.78) was derived
using classical physics, which breaks down at low temperatures. Thus, we would
not expect this equation to give a sensible answer close to the absolute zero of temperature.
, which contradicts
the
third law of thermodynamics. However,
this is not a problem. Equation (7.78) was derived
using classical physics, which breaks down at low temperatures. Thus, we would
not expect this equation to give a sensible answer close to the absolute zero of temperature.
![]() when the size of the system under consideration is
increased by the same factor. Intensive quantities stay the same. Energy and volume
are typical extensive quantities. Pressure and temperature are typical intensive
quantities. Entropy is very definitely an extensive quantity. We have previously shown
that the entropies of two weakly-interacting systems
are additive. [See Equation (7.62).] Thus, if we double the size of a system then we expect the
entropy to double as well. Suppose that we have a system of
volume
when the size of the system under consideration is
increased by the same factor. Intensive quantities stay the same. Energy and volume
are typical extensive quantities. Pressure and temperature are typical intensive
quantities. Entropy is very definitely an extensive quantity. We have previously shown
that the entropies of two weakly-interacting systems
are additive. [See Equation (7.62).] Thus, if we double the size of a system then we expect the
entropy to double as well. Suppose that we have a system of
volume ![]() , containing
, containing ![]() moles of ideal gas at temperature
moles of ideal gas at temperature ![]() . Doubling
the size of the system is like joining two identical systems together to
form a new system of volume
. Doubling
the size of the system is like joining two identical systems together to
form a new system of volume ![]() , containing
, containing ![]() moles of gas at temperature
moles of gas at temperature ![]() .
Let
.
Let
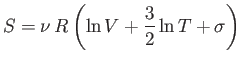
![$\displaystyle S' = 2 \nu R \left[\ln (2 V) + \frac{3}{2} \ln T + \sigma\right]$](img1413.png)
![]() after the partition is removed. Suppose, now, that the second system
is identical to the first system in all
respects, except that its molecules are in some way slightly
different to the molecules in the first system, so that the two sets of
molecules are distinguishable.
In this case, we would certainly expect an overall
increase in
entropy when the partition is removed. Before the partition is removed,
it separates type 1 molecules from type 2 molecules.
After the partition is removed, molecules of both
types become jumbled together. This is clearly an
irreversible process. We cannot imagine the molecules spontaneously sorting
themselves out again. The increase in entropy associated with this jumbling is
called entropy of mixing, and is easily calculated. We know that the number
of accessible states of an ideal gas varies with volume like
after the partition is removed. Suppose, now, that the second system
is identical to the first system in all
respects, except that its molecules are in some way slightly
different to the molecules in the first system, so that the two sets of
molecules are distinguishable.
In this case, we would certainly expect an overall
increase in
entropy when the partition is removed. Before the partition is removed,
it separates type 1 molecules from type 2 molecules.
After the partition is removed, molecules of both
types become jumbled together. This is clearly an
irreversible process. We cannot imagine the molecules spontaneously sorting
themselves out again. The increase in entropy associated with this jumbling is
called entropy of mixing, and is easily calculated. We know that the number
of accessible states of an ideal gas varies with volume like
![]() . The volume accessible to type 1 molecules clearly doubles after the
partition is removed, as does the volume accessible to type 2 molecules.
Using the fundamental formula
. The volume accessible to type 1 molecules clearly doubles after the
partition is removed, as does the volume accessible to type 2 molecules.
Using the fundamental formula
![]() , the increase in entropy
due to mixing is given by
, the increase in entropy
due to mixing is given by
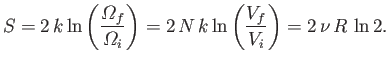
![]() ,
that appears when we
double the size of an ideal gas
system, by joining together two identical systems,
is entropy of mixing of the molecules contained in the original systems.
But, if the
molecules in these two systems are indistinguishable then why should there be any
entropy of mixing? Obviously, there is no entropy of mixing in this case.
At this point, we can begin to understand what has gone wrong in our calculation.
We have calculated the partition function assuming
that all of the molecules in our system have the
same mass and temperature, but we have not explicitly taken into account
the fact that we consider the molecules to be indistinguishable.
In other words, we have been treating the molecules in our ideal gas as if each
carried a little license plate, or a social security number, so that we could always
tell one from another. In quantum mechanics,
which is what we really should be using to study microscopic phenomena, the
essential indistinguishability of atoms and molecules is hard-wired into the
theory at a very low level. Our problem is that we have been taking the classical
approach a little too seriously. It is plainly nonsense to pretend that we can
distinguish molecules in a statistical problem where we cannot closely
follow the motions
of individual particles. A paradox arises if we try to treat molecules
as if they were distinguishable. This is called Gibb's paradox, after
the American physicist Josiah Gibbs, who first discussed it. The resolution
of Gibb's paradox is quite simple: treat all molecules of the same species
as if they were indistinguishable.
,
that appears when we
double the size of an ideal gas
system, by joining together two identical systems,
is entropy of mixing of the molecules contained in the original systems.
But, if the
molecules in these two systems are indistinguishable then why should there be any
entropy of mixing? Obviously, there is no entropy of mixing in this case.
At this point, we can begin to understand what has gone wrong in our calculation.
We have calculated the partition function assuming
that all of the molecules in our system have the
same mass and temperature, but we have not explicitly taken into account
the fact that we consider the molecules to be indistinguishable.
In other words, we have been treating the molecules in our ideal gas as if each
carried a little license plate, or a social security number, so that we could always
tell one from another. In quantum mechanics,
which is what we really should be using to study microscopic phenomena, the
essential indistinguishability of atoms and molecules is hard-wired into the
theory at a very low level. Our problem is that we have been taking the classical
approach a little too seriously. It is plainly nonsense to pretend that we can
distinguish molecules in a statistical problem where we cannot closely
follow the motions
of individual particles. A paradox arises if we try to treat molecules
as if they were distinguishable. This is called Gibb's paradox, after
the American physicist Josiah Gibbs, who first discussed it. The resolution
of Gibb's paradox is quite simple: treat all molecules of the same species
as if they were indistinguishable.
![]() molecules in the gas as distinguishable. Because of this,
we over-counted the
number of states of the system. Because the
molecules in the gas as distinguishable. Because of this,
we over-counted the
number of states of the system. Because the ![]() possible permutations of the
molecules amongst themselves do not lead to physically different situations,
and, therefore, cannot be counted as separate states, the number of actual states of
the system is a factor
possible permutations of the
molecules amongst themselves do not lead to physically different situations,
and, therefore, cannot be counted as separate states, the number of actual states of
the system is a factor ![]() less than what we initially thought. We can
easily correct our partition function by simply dividing by this factor, so that
less than what we initially thought. We can
easily correct our partition function by simply dividing by this factor, so that
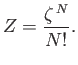
![$\displaystyle S = \nu R\left[ \ln V - \frac{3}{2} \ln \beta +\frac{3}{2} \ln\left(\frac{2\pi m k}{h_0^{ 2}}\right) + \frac{3}{2}\right]+ k (-N\ln N + N).$](img1424.png)