


Next: Ideal Monatomic Gas
Up: Applications of Statistical Thermodynamics
Previous: Calculation of Mean Values
Partition Function
It is clear that all important macroscopic quantities
associated with a system can be expressed in terms
of its partition function, 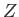 . Let us investigate how
the partition function is related to thermodynamical quantities.
Recall that
. Let us investigate how
the partition function is related to thermodynamical quantities.
Recall that 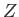 is a function of both
is a function of both 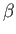 and
and  (where
(where  is the single
external parameter). Hence,
is the single
external parameter). Hence,
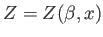 , and we can write
, and we can write
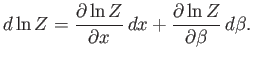 |
(7.51) |
Consider a quasi-static change by which  and
and 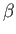 change so slowly that
the system stays close to equilibrium, and, thus, remains
distributed according to the
canonical distribution. It follows from Equations (7.35) and (7.45) that
change so slowly that
the system stays close to equilibrium, and, thus, remains
distributed according to the
canonical distribution. It follows from Equations (7.35) and (7.45) that
 |
(7.52) |
The last term can be rewritten
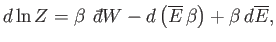 |
(7.53) |
giving
 |
(7.54) |
The previous equation shows that although the heat absorbed by the system,
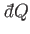 , is not
an exact differential, it becomes one when multiplied by the temperature
parameter,
, is not
an exact differential, it becomes one when multiplied by the temperature
parameter, 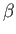 . This is essentially the second law of thermodynamics. In fact,
we know that
. This is essentially the second law of thermodynamics. In fact,
we know that
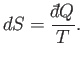 |
(7.55) |
Hence,
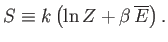 |
(7.56) |
This expression enables us to calculate the entropy of a system
from its partition function.
Suppose that we are dealing with a system  consisting of
two systems
consisting of
two systems  and
and  that only interact weakly with one another. Let each
state of
that only interact weakly with one another. Let each
state of  be denoted by an index
be denoted by an index  , and have a corresponding energy
, and have a corresponding energy 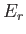 .
Likewise, let each state of
.
Likewise, let each state of  be denoted by an index
be denoted by an index  , and have a corresponding
energy
, and have a corresponding
energy 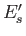 . A state of the combined system
. A state of the combined system 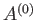 is then denoted
by two indices
is then denoted
by two indices  and
and  . Because
. Because  and
and  only interact weakly, their
energies are additive, and the energy of state
only interact weakly, their
energies are additive, and the energy of state  is
is
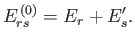 |
(7.57) |
By definition, the partition function of 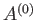 takes the form
takes the form
Hence,
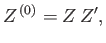 |
(7.59) |
giving
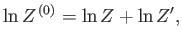 |
(7.60) |
where 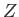 and
and 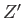 are the partition functions of
are the partition functions of  and
and  , respectively.
It follows from Equation (7.35) that the mean energies of
, respectively.
It follows from Equation (7.35) that the mean energies of 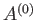 ,
,  , and
, and  are related by
are related by
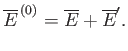 |
(7.61) |
It also follows from Equation (7.56) that the respective entropies of these systems
are related via
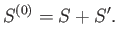 |
(7.62) |
Hence, the partition function tells us that the extensive (see Section 7.8) thermodynamic
functions of two weakly-interacting systems are simply additive.
It is clear that we can perform statistical thermodynamical calculations using
the partition function, 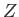 , instead of the more direct approach in which we use the
density of states,
, instead of the more direct approach in which we use the
density of states,
 . The former
approach is advantageous because the partition function
is an unrestricted sum of Boltzmann factors taken over all
accessible states,
irrespective of their energy, whereas the
density of states is a restricted sum taken over all states whose energies
lie in some narrow range. In general, it is far easier to perform an unrestricted
sum than a restricted sum. Thus, it is invariably more straightforward to derive
statistical thermodynamical results using
. The former
approach is advantageous because the partition function
is an unrestricted sum of Boltzmann factors taken over all
accessible states,
irrespective of their energy, whereas the
density of states is a restricted sum taken over all states whose energies
lie in some narrow range. In general, it is far easier to perform an unrestricted
sum than a restricted sum. Thus, it is invariably more straightforward to derive
statistical thermodynamical results using 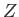 rather than
rather than
 , although
, although
 has a far more direct physical significance than
has a far more direct physical significance than 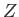 .
.



Next: Ideal Monatomic Gas
Up: Applications of Statistical Thermodynamics
Previous: Calculation of Mean Values
Richard Fitzpatrick
2016-01-25
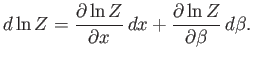
![]() consisting of
two systems
consisting of
two systems ![]() and
and ![]() that only interact weakly with one another. Let each
state of
that only interact weakly with one another. Let each
state of ![]() be denoted by an index
be denoted by an index ![]() , and have a corresponding energy
, and have a corresponding energy ![]() .
Likewise, let each state of
.
Likewise, let each state of ![]() be denoted by an index
be denoted by an index ![]() , and have a corresponding
energy
, and have a corresponding
energy ![]() . A state of the combined system
. A state of the combined system ![]() is then denoted
by two indices
is then denoted
by two indices ![]() and
and ![]() . Because
. Because ![]() and
and ![]() only interact weakly, their
energies are additive, and the energy of state
only interact weakly, their
energies are additive, and the energy of state ![]() is
is
![$\displaystyle = \sum_{r,s} \exp\left[-\beta E_{rs}^{ (0)}\right]= \sum_{r,s} \exp(-\beta [E_r+E_s'])= \sum_{r,s} \exp(-\beta E_r) \exp(-\beta E_s')$](img1380.png)
![$\displaystyle = \left[\sum_r \exp(-\beta E_r)\right]\left[\sum_s \exp(-\beta E_s')\right].$](img1381.png)
![]() , instead of the more direct approach in which we use the
density of states,
, instead of the more direct approach in which we use the
density of states,
![]() . The former
approach is advantageous because the partition function
is an unrestricted sum of Boltzmann factors taken over all
accessible states,
irrespective of their energy, whereas the
density of states is a restricted sum taken over all states whose energies
lie in some narrow range. In general, it is far easier to perform an unrestricted
sum than a restricted sum. Thus, it is invariably more straightforward to derive
statistical thermodynamical results using
. The former
approach is advantageous because the partition function
is an unrestricted sum of Boltzmann factors taken over all
accessible states,
irrespective of their energy, whereas the
density of states is a restricted sum taken over all states whose energies
lie in some narrow range. In general, it is far easier to perform an unrestricted
sum than a restricted sum. Thus, it is invariably more straightforward to derive
statistical thermodynamical results using ![]() rather than
rather than
![]() , although
, although
![]() has a far more direct physical significance than
has a far more direct physical significance than ![]() .
.