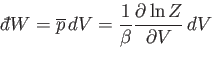Next: Partition Function
Up: Applications of Statistical Thermodynamics
Previous: System with Specified Mean
Consider a
system in contact with a heat reservoir, or with a specified mean energy. The systems in the representative
ensemble are distributed over their accessible states in accordance with the
canonical distribution.
Thus, the probability of occurrence of some state 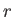 with energy
with energy 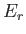 is given by
is given by
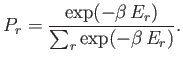 |
(7.31) |
The mean energy is written
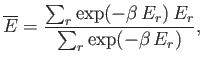 |
(7.32) |
where the sum is taken over all states of the system,
irrespective of their energy. Note that
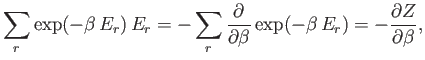 |
(7.33) |
where
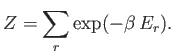 |
(7.34) |
It follows that
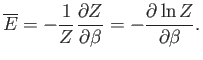 |
(7.35) |
The quantity 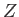 , which is defined as the sum of the Boltzmann factor over all
states, irrespective of their energy,
is called the partition function. (Incidentally, the partition function is represented by the symbol
, which is defined as the sum of the Boltzmann factor over all
states, irrespective of their energy,
is called the partition function. (Incidentally, the partition function is represented by the symbol 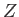 because in German it is
known as the ``zustandssumme,'' which means the ``sum over states.'')
We have just demonstrated that it is fairly easy to work out the
mean energy of a system using its partition function. In fact, as we shall
discover, it is straightforward
to calculate virtually any piece of statistical information from the partition
function.
because in German it is
known as the ``zustandssumme,'' which means the ``sum over states.'')
We have just demonstrated that it is fairly easy to work out the
mean energy of a system using its partition function. In fact, as we shall
discover, it is straightforward
to calculate virtually any piece of statistical information from the partition
function.
Let us evaluate the variance of the energy. We know
that
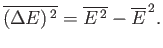 |
(7.36) |
(See Chapter 2.)
Now, according to the canonical distribution,
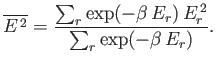 |
(7.37) |
However,
![$\displaystyle \sum_r \exp(-\beta E_r) E_r^{ 2} = -\frac{\partial} {\partial...
...rac{\partial}{\partial \beta}\right)^2 \left[ \sum_r \exp(-\beta E_r)\right].$](img1352.png) |
(7.38) |
Hence,
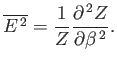 |
(7.39) |
We can also write
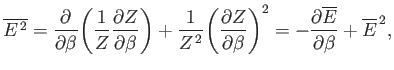 |
(7.40) |
where use has been made of Equation (7.35). It follows from Equation (7.36) that
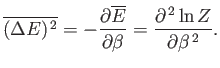 |
(7.41) |
Thus, the variance of the energy can be worked out from the partition function
almost as easily as the mean energy. Because, by definition,
a variance can never be negative, it
follows that
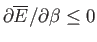 , or, equivalently,
, or, equivalently,
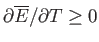 . Hence, the mean energy of a system
governed by the canonical distribution always increases with increasing temperature.
. Hence, the mean energy of a system
governed by the canonical distribution always increases with increasing temperature.
Suppose that the system is characterized by a single external parameter
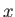 (such as
its volume). The generalization to the case where there are several external
parameters is straightforward. Consider a quasi-static change of the external parameter
from
(such as
its volume). The generalization to the case where there are several external
parameters is straightforward. Consider a quasi-static change of the external parameter
from 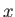 to
to 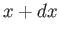 . In this process, the energy of the system in state
. In this process, the energy of the system in state 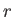 changes
by
changes
by
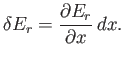 |
(7.42) |
The macroscopic work
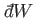 done by the system due to this parameter
change is
done by the system due to this parameter
change is
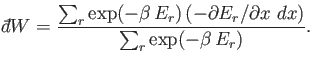 |
(7.43) |
In other words, the work done is minus the average change in internal
energy of the system, where the
average is calculated using the canonical distribution. We can write
![$\displaystyle \sum_r \exp(-\beta E_r) \frac{\partial E_r}{\partial x} = -\fr...
...m_r \exp(-\beta E_r)\right] = -\frac{1}{\beta} \frac{\partial Z}{\partial x},$](img1360.png) |
(7.44) |
which gives
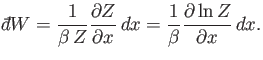 |
(7.45) |
We also have the following general expression for the work done by the system
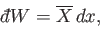 |
(7.46) |
where
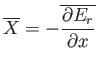 |
(7.47) |
is the mean generalized force conjugate to 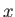 . (See Chapter 4.) It follows that
. (See Chapter 4.) It follows that
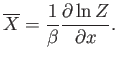 |
(7.48) |
Suppose that the external parameter is the volume, so 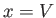 . It follows that
. It follows that
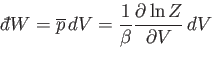 |
(7.49) |
and
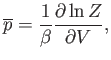 |
(7.50) |
where 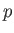 is the pressure.
Because the partition function is a function of
is the pressure.
Because the partition function is a function of 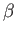 and
and  (the energies
(the energies
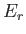 depend on
depend on  ), it follows that the previous equation relates
the mean pressure,
), it follows that the previous equation relates
the mean pressure,
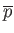 , to
, to  (via
(via
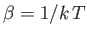 ) and
) and  . In other words, the previous expression
is the equation
of state. Hence, we can work out the pressure, and even the equation of state,
using the partition function.
. In other words, the previous expression
is the equation
of state. Hence, we can work out the pressure, and even the equation of state,
using the partition function.



Next: Partition Function
Up: Applications of Statistical Thermodynamics
Previous: System with Specified Mean
Richard Fitzpatrick
2016-01-25
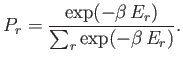
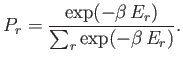
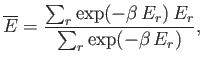
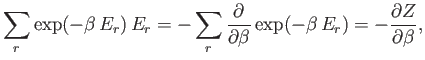
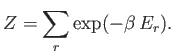
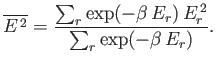
![$\displaystyle \sum_r \exp(-\beta E_r) E_r^{ 2} = -\frac{\partial} {\partial...
...rac{\partial}{\partial \beta}\right)^2 \left[ \sum_r \exp(-\beta E_r)\right].$](img1352.png)
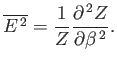
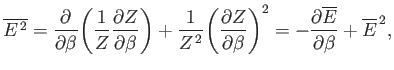
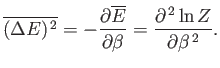
![]() (such as
its volume). The generalization to the case where there are several external
parameters is straightforward. Consider a quasi-static change of the external parameter
from
(such as
its volume). The generalization to the case where there are several external
parameters is straightforward. Consider a quasi-static change of the external parameter
from ![]() to
to ![]() . In this process, the energy of the system in state
. In this process, the energy of the system in state ![]() changes
by
changes
by
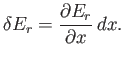
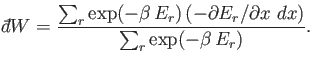
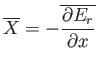
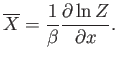
![]() . It follows that
. It follows that