


Next: Calculation of Mean Values
Up: Applications of Statistical Thermodynamics
Previous: Spin-1/2 Paramagnetism
System with Specified Mean Energy
Consider an isolated system,  , that consists of a fixed number of particles contained in a given volume.
Suppose that the the only available information about the system's energy is its mean value,
, that consists of a fixed number of particles contained in a given volume.
Suppose that the the only available information about the system's energy is its mean value,
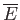 .
This might be the case, for example, if the system is brought to some final macrostate as a result of interaction with other
macroscopic systems. Here, the measurement of the macroscopic work done on the system, or the heat that it absorbs, during this process
does not tell us about the energy of each system in the corresponding ensemble, but, instead, only provides information about the
mean energy of the final macrostate of
.
This might be the case, for example, if the system is brought to some final macrostate as a result of interaction with other
macroscopic systems. Here, the measurement of the macroscopic work done on the system, or the heat that it absorbs, during this process
does not tell us about the energy of each system in the corresponding ensemble, but, instead, only provides information about the
mean energy of the final macrostate of  .
.
A system,  , with specified mean energy,
, with specified mean energy,
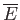 , is also described by a canonical distribution. For, if
such a system were placed in thermal contact with a heat reservoir held at some ``temperature,''
, is also described by a canonical distribution. For, if
such a system were placed in thermal contact with a heat reservoir held at some ``temperature,''
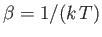 , then the mean
energy of the system would be determined. Thus, an appropriate choice of
, then the mean
energy of the system would be determined. Thus, an appropriate choice of 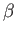 would guarantee that the mean energy of the system
had the specific value
would guarantee that the mean energy of the system
had the specific value
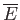 .
.
We can give a more direct proof of the previous assertion. Let 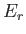 be the energy of system
be the energy of system  in some state
in some state 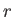 . Suppose that
the statistical ensemble consists of a very large number,
. Suppose that
the statistical ensemble consists of a very large number, 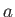 , of such systems,
, of such systems, 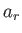 of which are in state
of which are in state 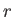 . Thus, the information
available to us is that
. Thus, the information
available to us is that
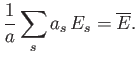 |
(7.27) |
Hence, it follows that
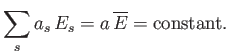 |
(7.28) |
This implies that the situation is equivalent to one in which a fixed amount of energy,
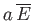 , is to
be distributed over all the systems in the ensemble, such that each system is equally likely to be in any one state.
If a system in the ensemble is in state
, is to
be distributed over all the systems in the ensemble, such that each system is equally likely to be in any one state.
If a system in the ensemble is in state 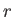 then the remaining
then the remaining 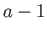 systems must then have a combined energy
systems must then have a combined energy
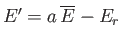 .
These
.
These 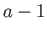 systems are distributed over some very large number,
systems are distributed over some very large number,
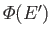 , of accessible states. In other words, if the one system under consideration is in state
, of accessible states. In other words, if the one system under consideration is in state 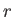 then the remaining
then the remaining 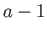 systems are distributed with equal probability in any of the
systems are distributed with equal probability in any of the
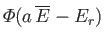 states accessible to them. Because
states accessible to them. Because
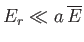 , the
mathematical problem here is exactly the same as that considered in Section 7.2, where we dealt with a system in thermal contact with
a heat bath. In this case, the role of the heat bath is played by the totality of all the other systems in the ensemble. Accordingly, we again
get the canonical distribution,
, the
mathematical problem here is exactly the same as that considered in Section 7.2, where we dealt with a system in thermal contact with
a heat bath. In this case, the role of the heat bath is played by the totality of all the other systems in the ensemble. Accordingly, we again
get the canonical distribution,
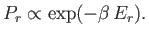 |
(7.29) |
The parameter
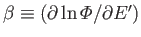 does not here have any immediate physical
significance in terms of the temperature of a real heat bath. Instead, it is to be determined by the
condition that the mean energy calculated using the distribution has the specified value
does not here have any immediate physical
significance in terms of the temperature of a real heat bath. Instead, it is to be determined by the
condition that the mean energy calculated using the distribution has the specified value
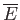 .
In other words,
.
In other words,
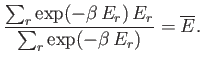 |
(7.30) |
In conclusion, if one is dealing with a system in contact with a heat bath held at ``temperature''
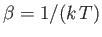 then the canonical distribution,
(7.29), is valid, and the mean energy,
then the canonical distribution,
(7.29), is valid, and the mean energy,
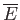 , can be calculated from Equation (7.30), using the known value of
, can be calculated from Equation (7.30), using the known value of 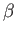 .
On the other hand, if one is dealing with a system of specified mean energy,
.
On the other hand, if one is dealing with a system of specified mean energy,
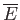 , then the canonical distribution, (7.29), is again
valid, but the parameter
, then the canonical distribution, (7.29), is again
valid, but the parameter 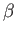 is to be calculated using Equation (7.30) and the known value of
is to be calculated using Equation (7.30) and the known value of
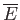 .
.



Next: Calculation of Mean Values
Up: Applications of Statistical Thermodynamics
Previous: Spin-1/2 Paramagnetism
Richard Fitzpatrick
2016-01-25
![]() , with specified mean energy,
, with specified mean energy,
![]() , is also described by a canonical distribution. For, if
such a system were placed in thermal contact with a heat reservoir held at some ``temperature,''
, is also described by a canonical distribution. For, if
such a system were placed in thermal contact with a heat reservoir held at some ``temperature,''
![]() , then the mean
energy of the system would be determined. Thus, an appropriate choice of
, then the mean
energy of the system would be determined. Thus, an appropriate choice of ![]() would guarantee that the mean energy of the system
had the specific value
would guarantee that the mean energy of the system
had the specific value
![]() .
.
![]() be the energy of system
be the energy of system ![]() in some state
in some state ![]() . Suppose that
the statistical ensemble consists of a very large number,
. Suppose that
the statistical ensemble consists of a very large number, ![]() , of such systems,
, of such systems, ![]() of which are in state
of which are in state ![]() . Thus, the information
available to us is that
. Thus, the information
available to us is that
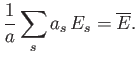
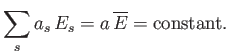
![]() then the canonical distribution,
(7.29), is valid, and the mean energy,
then the canonical distribution,
(7.29), is valid, and the mean energy,
![]() , can be calculated from Equation (7.30), using the known value of
, can be calculated from Equation (7.30), using the known value of ![]() .
On the other hand, if one is dealing with a system of specified mean energy,
.
On the other hand, if one is dealing with a system of specified mean energy,
![]() , then the canonical distribution, (7.29), is again
valid, but the parameter
, then the canonical distribution, (7.29), is again
valid, but the parameter ![]() is to be calculated using Equation (7.30) and the known value of
is to be calculated using Equation (7.30) and the known value of
![]() .
.