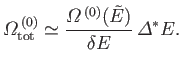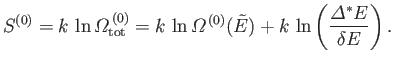Next: Uses of Entropy
Up: Statistical Thermodynamics
Previous: Entropy
Properties of Entropy
Entropy, as we have defined it, has some dependence on the resolution,  ,
to which the energy of macrostates is measured. Recall that
,
to which the energy of macrostates is measured. Recall that
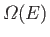 is the
number of accessible microstates with energy in the range
is the
number of accessible microstates with energy in the range  to
to
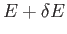 .
Suppose that we choose a new resolution
.
Suppose that we choose a new resolution
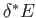 , and define a new
density of states,
, and define a new
density of states,
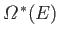 , which is the number of states with energy
in the range
, which is the number of states with energy
in the range  to
to
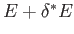 . It can easily be seen that
. It can easily be seen that
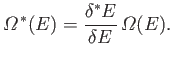 |
(5.70) |
It follows that the new entropy,
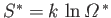 , is related to the
previous entropy
, is related to the
previous entropy
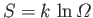 via
via
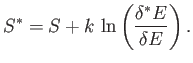 |
(5.71) |
Now, our usual estimate that
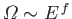 (see Section 3.8) gives
(see Section 3.8) gives
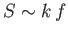 , where
, where
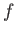 is the number of degrees of freedom. It follows that even if
is the number of degrees of freedom. It follows that even if
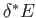 were to differ from
were to differ from 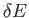 by of order
by of order 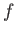 (i.e., twenty four orders of
magnitude), which is virtually inconceivable, the second term on the right-hand
side of the previous equation is still only of order
(i.e., twenty four orders of
magnitude), which is virtually inconceivable, the second term on the right-hand
side of the previous equation is still only of order 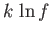 , which is utterly
negligible compared to
, which is utterly
negligible compared to 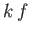 . It follows that
. It follows that
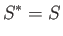 |
(5.72) |
to an excellent approximation, so our definition of entropy is completely
insensitive to the resolution to which we measure energy (or any other
macroscopic parameter).
Note that, like the
temperature, the entropy of a macrostate is only well defined if
the macrostate is in equilibrium. The crucial point is that
it only makes sense to talk about the
number of accessible states if the systems
in the ensemble are given sufficient time to thoroughly explore all of the possible
microstates consistent with the known
macroscopic constraints. In other words, we can only
be sure that a given microstate is inaccessible when the systems in the ensemble have
had ample opportunity to move into it, and yet have not done so. For an
equilibrium state, the entropy is just as well defined as more familiar quantities
such as the temperature and the mean pressure.
Consider, again, two systems,  and
and 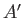 , that are in thermal contact, but can do
no work on one another. (See Section 5.2.)
Let
, that are in thermal contact, but can do
no work on one another. (See Section 5.2.)
Let  and
and 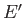 be the energies of the two systems,
and
be the energies of the two systems,
and
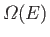 and
and
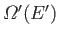 the respective densities of states.
Furthermore, let
the respective densities of states.
Furthermore, let 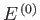 be the conserved energy of the
system as a whole, and
be the conserved energy of the
system as a whole, and
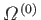 the corresponding density of states.
We have from Equation (5.2) that
the corresponding density of states.
We have from Equation (5.2) that
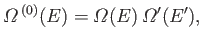 |
(5.73) |
where
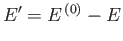 . In other words, the number of states accessible to the
whole system is the product of the numbers of states accessible to each subsystem,
because every microstate of
. In other words, the number of states accessible to the
whole system is the product of the numbers of states accessible to each subsystem,
because every microstate of  can be combined with every microstate of
can be combined with every microstate of
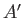 to form a distinct microstate of the whole system. We know, from Section 5.2,
that in equilibrium the mean energy of
to form a distinct microstate of the whole system. We know, from Section 5.2,
that in equilibrium the mean energy of  takes the value
takes the value
 for which
for which
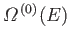 is maximum, and the
temperatures of
is maximum, and the
temperatures of  and
and 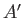 are equal. The distribution of
are equal. The distribution of  around the
mean value is of order
around the
mean value is of order
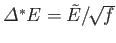 , where
, where 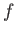 is the number of
degrees of freedom. It follows that the total number of accessible microstates is
approximately the number of states which lie within
is the number of
degrees of freedom. It follows that the total number of accessible microstates is
approximately the number of states which lie within
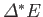 of
of 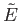 .
Thus,
.
Thus,
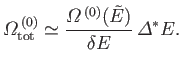 |
(5.74) |
The entropy of the whole system is given by
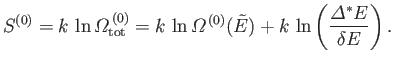 |
(5.75) |
According to our usual estimate,
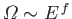 (see Section 3.8), the first term on the
right-hand
side of the previous equation is of order
(see Section 3.8), the first term on the
right-hand
side of the previous equation is of order 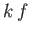 , whereas the second term is of order
, whereas the second term is of order
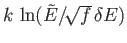 . Any reasonable choice for the energy subdivision,
. Any reasonable choice for the energy subdivision, 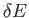 , should be
greater than
, should be
greater than
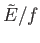 , otherwise there would
be less than one microstate per subdivision. It follows that the second term
is less than, or of order,
, otherwise there would
be less than one microstate per subdivision. It follows that the second term
is less than, or of order, 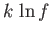 , which is utterly negligible compared to
, which is utterly negligible compared to
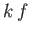 . Thus,
. Thus,
![$\displaystyle S^{(0)} = k \ln{\mit\Omega}^{ (0)}(\tilde{E}) = k \ln[{\mit\Om...
...\tilde{E}')] =k \ln {\mit\Omega}(\tilde{E}) + k \ln {\mit\Omega}'(\tilde{E}')$](img765.png) |
(5.76) |
to an excellent approximation,
giving
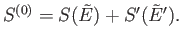 |
(5.77) |
It can be seen that the probability distribution for
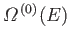 is so strongly peaked
around its maximum value that, for the purpose of calculating the entropy, the
total number of states is equal to the maximum number of states [i.e.,
is so strongly peaked
around its maximum value that, for the purpose of calculating the entropy, the
total number of states is equal to the maximum number of states [i.e.,
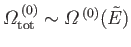 ].
One consequence
of this is that entropy possesses the simple additive property illustrated in
Equation (5.77). Thus, the total entropy of two thermally interacting systems
in equilibrium is the sum of the entropies of each system taken in isolation.
].
One consequence
of this is that entropy possesses the simple additive property illustrated in
Equation (5.77). Thus, the total entropy of two thermally interacting systems
in equilibrium is the sum of the entropies of each system taken in isolation.



Next: Uses of Entropy
Up: Statistical Thermodynamics
Previous: Entropy
Richard Fitzpatrick
2016-01-25
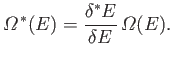
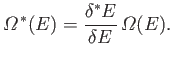
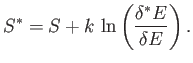
![]() and
and ![]() , that are in thermal contact, but can do
no work on one another. (See Section 5.2.)
Let
, that are in thermal contact, but can do
no work on one another. (See Section 5.2.)
Let ![]() and
and ![]() be the energies of the two systems,
and
be the energies of the two systems,
and
![]() and
and
![]() the respective densities of states.
Furthermore, let
the respective densities of states.
Furthermore, let ![]() be the conserved energy of the
system as a whole, and
be the conserved energy of the
system as a whole, and
![]() the corresponding density of states.
We have from Equation (5.2) that
the corresponding density of states.
We have from Equation (5.2) that