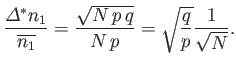Next: Gaussian Probability Distribution
Up: Probability Theory
Previous: Mean, Variance, and Standard
Let us now apply what we have just learned about the mean, variance, and
standard deviation of a general probability distribution function
to the specific case of the
binomial probability distribution. Recall, from Section 2.6,
that if a simple system has just two possible outcomes,
denoted 1 and 2, with
respective probabilities  and
and 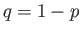 ,
then the probability of obtaining
,
then the probability of obtaining  occurrences of outcome 1 in
occurrences of outcome 1 in  observations is
observations is
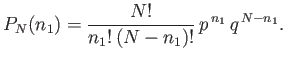 |
(2.38) |
Thus, making use of Equation (2.27), the mean number of occurrences of outcome 1 in  observations
is given by
observations
is given by
 |
(2.39) |
We can see that if the
final factor
 were absent on the right-hand side of the previous expression then it would just reduce to the binomial expansion, which we
know how to sum. [See Equation (2.23).] We can take advantage of this fact using a rather elegant
mathematical sleight of hand. Observe that because
were absent on the right-hand side of the previous expression then it would just reduce to the binomial expansion, which we
know how to sum. [See Equation (2.23).] We can take advantage of this fact using a rather elegant
mathematical sleight of hand. Observe that because
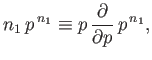 |
(2.40) |
the previous summation can be rewritten as
![$\displaystyle \sum_{n_1=0,N}\frac{N!}{n_1! (N-n_1)!} p^{ n_1} q^{ N-n_1} ...
...\left[\sum_{n_1=0,N} \frac{N!}{n_1! (N-n_1)!} p^{ n_1} q^{ N-n_1} \right].$](img186.png) |
(2.41) |
The term in square brackets is now the familiar binomial expansion, and
can be written more succinctly as
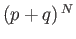 .
Thus,
.
Thus,
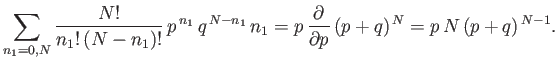 |
(2.42) |
However, 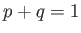 for the case in hand [see Equation (2.11)], so
for the case in hand [see Equation (2.11)], so
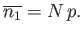 |
(2.43) |
In fact, we could have guessed the previous result.
By definition, the probability,  , is the number of occurrences of the
outcome 1 divided by the number of trials, in the limit as the number
of trials goes to infinity:
, is the number of occurrences of the
outcome 1 divided by the number of trials, in the limit as the number
of trials goes to infinity:
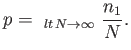 |
(2.44) |
If we think carefully, however,
we can see that taking the limit as the number
of trials goes to infinity is equivalent to taking the mean value,
so that
 |
(2.45) |
But, this is just a simple rearrangement of Equation (2.43).
Let us now calculate the variance of  . Recall, from Equation (2.36), that
. Recall, from Equation (2.36), that
 |
(2.46) |
We already know
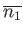 ,
so we just need to calculate
,
so we just need to calculate
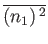 .
This average is written
.
This average is written
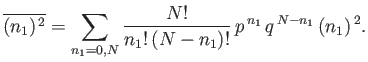 |
(2.47) |
The sum can be evaluated using a simple extension of the mathematical trick that
we used previously to evaluate
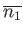 . Because
. Because
 |
(2.48) |
then
Using 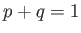 , we obtain
, we obtain
because
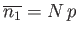 . [See Equation (2.43).] It follows that the variance
of
. [See Equation (2.43).] It follows that the variance
of  is given by
is given by
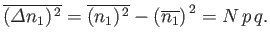 |
(2.51) |
The standard deviation of  is the square root of the variance [see Equation (2.37)], so that
is the square root of the variance [see Equation (2.37)], so that
 |
(2.52) |
Recall that this quantity is essentially the width of the range over which
 is distributed around its mean value. The relative width of the
distribution is characterized by
is distributed around its mean value. The relative width of the
distribution is characterized by
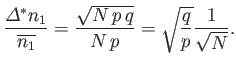 |
(2.53) |
It is clear, from this formula, that the relative width decreases with increasing  like
like
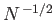 . So, the greater the number of trials, the
more likely it is that an observation of
. So, the greater the number of trials, the
more likely it is that an observation of  will yield a result
that is relatively close to the mean value,
will yield a result
that is relatively close to the mean value,
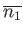 .
.



Next: Gaussian Probability Distribution
Up: Probability Theory
Previous: Mean, Variance, and Standard
Richard Fitzpatrick
2016-01-25
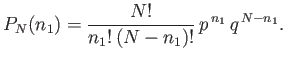

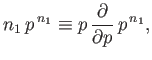
![$\displaystyle \sum_{n_1=0,N}\frac{N!}{n_1! (N-n_1)!} p^{ n_1} q^{ N-n_1} ...
...\left[\sum_{n_1=0,N} \frac{N!}{n_1! (N-n_1)!} p^{ n_1} q^{ N-n_1} \right].$](img186.png)
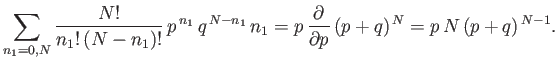
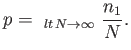

![]() . Recall, from Equation (2.36), that
. Recall, from Equation (2.36), that
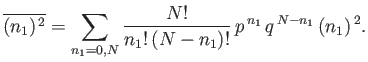

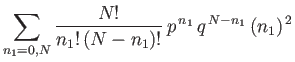
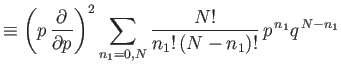
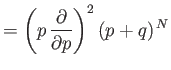
![$\displaystyle =\left(p \frac{\partial}{\partial p}\right)\left[p N (p+q)^{ N-1}\right]$](img199.png)
![]() is the square root of the variance [see Equation (2.37)], so that
is the square root of the variance [see Equation (2.37)], so that