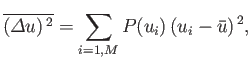Next: Application to Binomial Probability
Up: Probability Theory
Previous: Binomial Probability Distribution
What is meant by the mean, or average, of a quantity? Suppose that we
wanted to calculate the average age of undergraduates at the University of Texas at Austin.
We could go to the central administration building, and find
out how many eighteen year-olds, nineteen year-olds, et cetera, were currently
enrolled. We would then write something like
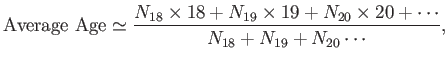 |
(2.24) |
where 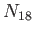 is the number of enrolled eighteen year-olds, et cetera.
Suppose that we were to pick a student at random and then ask ``What is
the probability of this student being eighteen?'' From what we have
already discussed, this probability is defined
is the number of enrolled eighteen year-olds, et cetera.
Suppose that we were to pick a student at random and then ask ``What is
the probability of this student being eighteen?'' From what we have
already discussed, this probability is defined
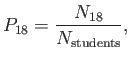 |
(2.25) |
where
 is the total number of enrolled
students.
We can now see that the average age takes
the form
is the total number of enrolled
students.
We can now see that the average age takes
the form
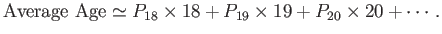 |
(2.26) |
There is nothing special about the age distribution of students
at UT Austin. So, for a general variable 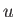 , which can take on any one of
, which can take on any one of 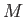 possible values,
possible values, 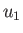 ,
,
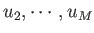 , with corresponding probabilities
, with corresponding probabilities
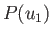 ,
,
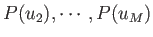 ,
the mean, or average, value of
,
the mean, or average, value of 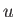 , which
is denoted
, which
is denoted 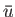 , is defined as
, is defined as
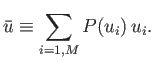 |
(2.27) |
Suppose that 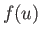 is some function of
is some function of 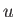 . For each of
the
. For each of
the 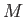 possible values of
possible values of 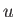 , there is a corresponding value
of
, there is a corresponding value
of 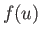 that occurs with the same probability. Thus,
that occurs with the same probability. Thus, 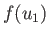 corresponds
to
corresponds
to 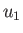 , and occurs with the probability
, and occurs with the probability 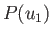 , and so on. It follows from
our previous definition that the mean value of
, and so on. It follows from
our previous definition that the mean value of 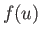 is
given by
is
given by
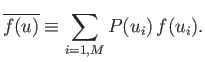 |
(2.28) |
Suppose that 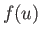 and
and 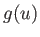 are two general functions of
are two general functions of 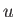 . It follows that
. It follows that
![$\displaystyle \overline{f(u)+g(u)} = \sum_{i=1,M}P(u_i) [f(u_i)+g(u_i)] = \sum_{i=1,M}P(u_i) f(u_i)+ \sum_{i=1,M}P(u_i) g(u_i),$](img174.png) |
(2.29) |
so that
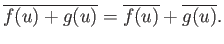 |
(2.30) |
Finally, if 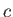 is a general constant then it is clear that
is a general constant then it is clear that
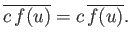 |
(2.31) |
We now know how to define the mean value of the general variable 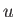 .
But, how can we characterize the scatter around the mean value?
We could investigate the deviation of
.
But, how can we characterize the scatter around the mean value?
We could investigate the deviation of 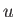 from its mean value,
from its mean value, 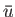 ,
which is denoted
,
which is denoted
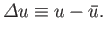 |
(2.32) |
In fact, this is not a particularly interesting quantity, because its average
is obviously zero:
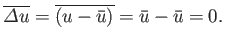 |
(2.33) |
This is another way of saying that the average deviation from the
mean vanishes. A more interesting quantity is the square of the
deviation. The average value of this quantity,
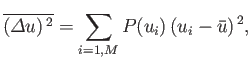 |
(2.34) |
is usually called the
variance.
The variance is clearly a positive number,
unless there is no scatter at all in the
distribution, so that all possible values of 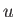 correspond to the
mean value,
correspond to the
mean value, 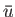 , in which case it is zero.
The following general relation
is often useful
, in which case it is zero.
The following general relation
is often useful
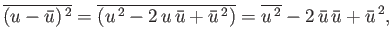 |
(2.35) |
giving
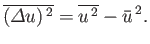 |
(2.36) |
The variance of 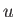 is proportional to the square of the scatter
of
is proportional to the square of the scatter
of 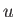 around its mean value. A more useful measure of the scatter
is given by the square root of the variance,
around its mean value. A more useful measure of the scatter
is given by the square root of the variance,
![$\displaystyle {\mit\Delta}^\ast u = \left[\overline{({\mit\Delta} u)^{ 2}}\right]^{1/2},$](img183.png) |
(2.37) |
which is usually called the standard deviation of 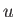 . The
standard deviation is essentially the width of the range over which
. The
standard deviation is essentially the width of the range over which
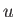 is distributed around its mean value,
is distributed around its mean value, 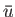 .
.



Next: Application to Binomial Probability
Up: Probability Theory
Previous: Binomial Probability Distribution
Richard Fitzpatrick
2016-01-25
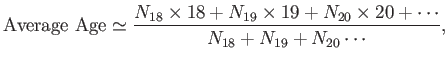
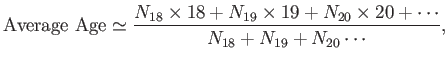
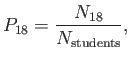
![]() , which can take on any one of
, which can take on any one of ![]() possible values,
possible values, ![]() ,
,
![]() , with corresponding probabilities
, with corresponding probabilities
![]() ,
,
![]() ,
the mean, or average, value of
,
the mean, or average, value of ![]() , which
is denoted
, which
is denoted ![]() , is defined as
, is defined as
![]() is some function of
is some function of ![]() . For each of
the
. For each of
the ![]() possible values of
possible values of ![]() , there is a corresponding value
of
, there is a corresponding value
of ![]() that occurs with the same probability. Thus,
that occurs with the same probability. Thus, ![]() corresponds
to
corresponds
to ![]() , and occurs with the probability
, and occurs with the probability ![]() , and so on. It follows from
our previous definition that the mean value of
, and so on. It follows from
our previous definition that the mean value of ![]() is
given by
is
given by
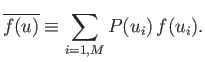
![$\displaystyle \overline{f(u)+g(u)} = \sum_{i=1,M}P(u_i) [f(u_i)+g(u_i)] = \sum_{i=1,M}P(u_i) f(u_i)+ \sum_{i=1,M}P(u_i) g(u_i),$](img174.png)
![]() .
But, how can we characterize the scatter around the mean value?
We could investigate the deviation of
.
But, how can we characterize the scatter around the mean value?
We could investigate the deviation of ![]() from its mean value,
from its mean value, ![]() ,
which is denoted
,
which is denoted