


Next: Phase Diagrams
Up: Multi-Phase Systems
Previous: Equilibrium Between Phases
It is possible to characterize the phase-equilibrium line in terms of a differential equation. Referring to Figure 9.1, consider a
point, such as  , that lies on the phase-equilibrium line, and corresponds to the temperature
, that lies on the phase-equilibrium line, and corresponds to the temperature  and the pressure
and the pressure  . The condition (9.63) implies that
. The condition (9.63) implies that
 |
(9.64) |
Now, consider
a neighboring point, such as  , that also lies on the phase-equilibrium line, and corresponds to the temperature
, that also lies on the phase-equilibrium line, and corresponds to the temperature 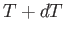 and
the pressure
and
the pressure 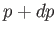 . The condition (9.63) yields
. The condition (9.63) yields
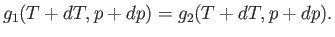 |
(9.65) |
Taking the difference between the previous two equations, we obtain
 |
(9.66) |
where
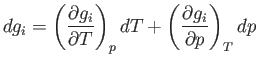 |
(9.67) |
is the change in Gibbs free energy per mole of phase  in going from point
in going from point  to point
to point  .
.
The change, 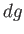 , for each phase can also be obtained from the fundamental thermodynamic relation
, for each phase can also be obtained from the fundamental thermodynamic relation
 |
(9.68) |
Here, 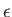 refers to molar energy (i.e., energy per mole),
refers to molar energy (i.e., energy per mole),  to molar entropy, and
to molar entropy, and  to molar volume. Thus,
to molar volume. Thus,
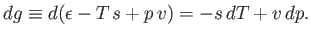 |
(9.69) |
Hence, Equation (9.66) implies that
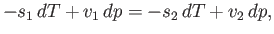 |
(9.70) |
or
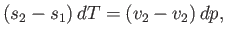 |
(9.71) |
which reduces to
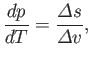 |
(9.72) |
where
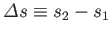 and
and
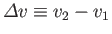 . This result is known as the Clausius-Clapeyron equation.
. This result is known as the Clausius-Clapeyron equation.
Consider any point on the phase-equilibrium line at temperature  and pressure
and pressure  . The Clausius-Clapeyron equation
then relates the local slope of the line to the molar entropy change,
. The Clausius-Clapeyron equation
then relates the local slope of the line to the molar entropy change,
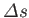 , and the molar volume change,
, and the molar volume change,
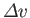 , of the
substance in crossing the line at this point. Note, incidentally, that the quantities on the right-hand side of the Clausius-Clapeyron equation
do not necessarily need to refer to one mole of the substance. In fact, both numerator and denominator can be multiplied by the
same number of moles, leaving
, of the
substance in crossing the line at this point. Note, incidentally, that the quantities on the right-hand side of the Clausius-Clapeyron equation
do not necessarily need to refer to one mole of the substance. In fact, both numerator and denominator can be multiplied by the
same number of moles, leaving 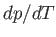 unchanged.
unchanged.
Because there is an entropy change associated with a phase transformation, heat must also be absorbed during such a process. The
latent heat of transformation,  , is defined as the heat absorbed when a given amount of phase 1 is
transformed to phase 2. Because this process takes place at the constant temperature
, is defined as the heat absorbed when a given amount of phase 1 is
transformed to phase 2. Because this process takes place at the constant temperature  , the corresponding entropy change is
, the corresponding entropy change is
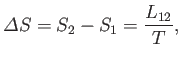 |
(9.73) |
where  is the latent heat at this temperature. Thus, the Clausius-Clapeyron equation, (9.72), can also
be written
is the latent heat at this temperature. Thus, the Clausius-Clapeyron equation, (9.72), can also
be written
 |
(9.74) |



Next: Phase Diagrams
Up: Multi-Phase Systems
Previous: Equilibrium Between Phases
Richard Fitzpatrick
2016-01-25
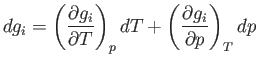
![]() , for each phase can also be obtained from the fundamental thermodynamic relation
, for each phase can also be obtained from the fundamental thermodynamic relation
![]() and pressure
and pressure ![]() . The Clausius-Clapeyron equation
then relates the local slope of the line to the molar entropy change,
. The Clausius-Clapeyron equation
then relates the local slope of the line to the molar entropy change,
![]() , and the molar volume change,
, and the molar volume change,
![]() , of the
substance in crossing the line at this point. Note, incidentally, that the quantities on the right-hand side of the Clausius-Clapeyron equation
do not necessarily need to refer to one mole of the substance. In fact, both numerator and denominator can be multiplied by the
same number of moles, leaving
, of the
substance in crossing the line at this point. Note, incidentally, that the quantities on the right-hand side of the Clausius-Clapeyron equation
do not necessarily need to refer to one mole of the substance. In fact, both numerator and denominator can be multiplied by the
same number of moles, leaving ![]() unchanged.
unchanged.
![]() , is defined as the heat absorbed when a given amount of phase 1 is
transformed to phase 2. Because this process takes place at the constant temperature
, is defined as the heat absorbed when a given amount of phase 1 is
transformed to phase 2. Because this process takes place at the constant temperature ![]() , the corresponding entropy change is
, the corresponding entropy change is