


Next: Vapor Pressure
Up: Multi-Phase Systems
Previous: Clausius-Clapeyron Equation
Simple substances are capable of existing in three different types of phase: namely, solid, liquid, and gas. (There may
actually be several solid phases with different crystal structures.) In the  -
- plane, the phase-equilibrium lines
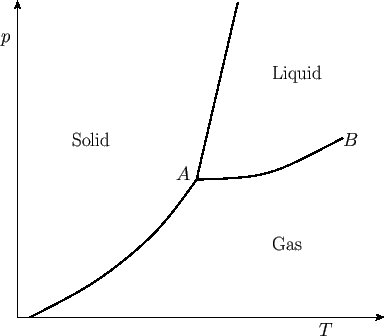
separating these phases typically appear as indicated in Figure 9.2. These lines separate solid
from liquid, liquid from gas, and solid from gas. The gas phase is sometimes called the vapor phase. The
transformation from solid to liquid is called melting, that from liquid to gas is called vaporization, and
that from solid to gas is called sublimation. The three phase-equilibrium lines meet at one
common point,
plane, the phase-equilibrium lines
separating these phases typically appear as indicated in Figure 9.2. These lines separate solid
from liquid, liquid from gas, and solid from gas. The gas phase is sometimes called the vapor phase. The
transformation from solid to liquid is called melting, that from liquid to gas is called vaporization, and
that from solid to gas is called sublimation. The three phase-equilibrium lines meet at one
common point,  , known as the triple point. At this unique temperature and pressure, arbitrary amounts of
all three phases can coexist in equilibrium. (This is the property that makes the triple point of water so suitable as
a readily reproducible temperature standard.) At point
, known as the triple point. At this unique temperature and pressure, arbitrary amounts of
all three phases can coexist in equilibrium. (This is the property that makes the triple point of water so suitable as
a readily reproducible temperature standard.) At point  , the so-called critical point, the liquid-gas
equilibrium line ends. The volume change,
, the so-called critical point, the liquid-gas
equilibrium line ends. The volume change,
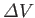 , between the liquid and gas phases is zero at this point.
Beyond point
, between the liquid and gas phases is zero at this point.
Beyond point  , there is no further phase transformation, because there exists a single fluid phase (i.e., the
very dense gas has become indistinguishable from the liquid.)
, there is no further phase transformation, because there exists a single fluid phase (i.e., the
very dense gas has become indistinguishable from the liquid.)
Figure:
Phase diagram for a simple substance. Point  is the triple point, and point
is the triple point, and point  is the
critical point.
is the
critical point.
 |
In going from solid ( ) to liquid (
) to liquid (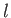 ), the entropy (or degree of disorder) of the substance almost always increases. Thus, the
corresponding latent heat,
), the entropy (or degree of disorder) of the substance almost always increases. Thus, the
corresponding latent heat, 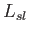 , is positive, and heat is absorbed in the transformation. In most cases, the solid
expands upon melting, so
, is positive, and heat is absorbed in the transformation. In most cases, the solid
expands upon melting, so
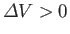 . In this case, the Clausius-Clapeyron equation, (9.74), asserts that the
slope of the solid-liquid equilibrium line (i.e., the melting curve) is positive, as shown in the diagram. However, there exist
some substances, such as water, that contract upon melting, so that
. In this case, the Clausius-Clapeyron equation, (9.74), asserts that the
slope of the solid-liquid equilibrium line (i.e., the melting curve) is positive, as shown in the diagram. However, there exist
some substances, such as water, that contract upon melting, so that
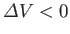 . For these substances, the
slope of the melting curve is negative.
. For these substances, the
slope of the melting curve is negative.



Next: Vapor Pressure
Up: Multi-Phase Systems
Previous: Clausius-Clapeyron Equation
Richard Fitzpatrick
2016-01-25


![]() ) to liquid (
) to liquid (![]() ), the entropy (or degree of disorder) of the substance almost always increases. Thus, the
corresponding latent heat,
), the entropy (or degree of disorder) of the substance almost always increases. Thus, the
corresponding latent heat, ![]() , is positive, and heat is absorbed in the transformation. In most cases, the solid
expands upon melting, so
, is positive, and heat is absorbed in the transformation. In most cases, the solid
expands upon melting, so
![]() . In this case, the Clausius-Clapeyron equation, (9.74), asserts that the
slope of the solid-liquid equilibrium line (i.e., the melting curve) is positive, as shown in the diagram. However, there exist
some substances, such as water, that contract upon melting, so that
. In this case, the Clausius-Clapeyron equation, (9.74), asserts that the
slope of the solid-liquid equilibrium line (i.e., the melting curve) is positive, as shown in the diagram. However, there exist
some substances, such as water, that contract upon melting, so that
![]() . For these substances, the
slope of the melting curve is negative.
. For these substances, the
slope of the melting curve is negative.