


Next: Clausius-Clapeyron Equation
Up: Multi-Phase Systems
Previous: Stability of Single-Phase Substance
Consider a system that consists of two phases, which we shall denote by 1 and 2. For example, these might be
solid and liquid, or liquid and gas. Suppose that the system is in equilibrium with a reservoir at the constant temperature  , and the
constant pressure
, and the
constant pressure  , so that the system always has the temperature
, so that the system always has the temperature  and the mean pressure
and the mean pressure  . However, the
system can exist in either one of its two phases, or some mixture of the two. Let us begin by finding the conditions that allow
the two phases to coexist in equilibrium with one another.
. However, the
system can exist in either one of its two phases, or some mixture of the two. Let us begin by finding the conditions that allow
the two phases to coexist in equilibrium with one another.
In accordance with the discussion in Section 9.4, the equilibrium condition is that the
Gibbs free energy, 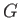 , of the system is a minimum:
, of the system is a minimum:
 |
(9.59) |
Let 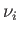 be the number of moles of phase
be the number of moles of phase  present in the system, and let
present in the system, and let 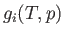 be the
Gibbs free energy per mole of phase
be the
Gibbs free energy per mole of phase  at the temperature
at the temperature  and the pressure
and the pressure  . It follows that
. It follows that
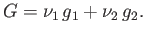 |
(9.60) |
Furthermore, the conservation of matter implies that the total number of moles, 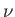 , of the substance
remains constant:
, of the substance
remains constant:
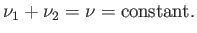 |
(9.61) |
Thus, we can take 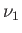 as the one independent parameter that is free to vary. In equilibrium, Equation (9.59) requires that
as the one independent parameter that is free to vary. In equilibrium, Equation (9.59) requires that
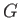 be stationary for small variations in
be stationary for small variations in 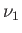 . In other words,
. In other words,
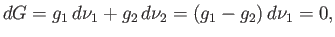 |
(9.62) |
because
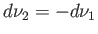 , as a consequence of Equation (9.61). Hence, a necessary condition for equilibrium between the two
phases is
, as a consequence of Equation (9.61). Hence, a necessary condition for equilibrium between the two
phases is
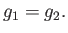 |
(9.63) |
Clearly, when this condition is satisfied then the transfer of a mole of substance from one phase to another does not
change the overall Gibbs free energy, 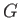 , of the system. Hence,
, of the system. Hence, 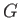 is stationary, as required. Incidentally, the
condition that
is stationary, as required. Incidentally, the
condition that 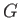 is a minimum (rather than a maximum) is easily shown to reduce to the requirement that the
heat capacities and isothermal compressibilities of both phases be positive, so that each phase is stable to temperature and volume fluctuations.
is a minimum (rather than a maximum) is easily shown to reduce to the requirement that the
heat capacities and isothermal compressibilities of both phases be positive, so that each phase is stable to temperature and volume fluctuations.
Figure 9.1:
Pressure-temperature plot showing the domains of relative stability of two phases, and the
phase-equilibrium line.
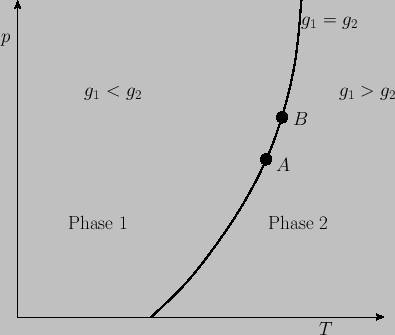 |
Now, for a given temperature and pressure, 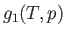 is a well-defined function characteristic of phase 1. Likewise,
is a well-defined function characteristic of phase 1. Likewise, 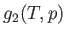 is a
well-defined function characteristic of phase 2. If
is a
well-defined function characteristic of phase 2. If  and
and  are such that
are such that 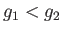 then the minimum value of
then the minimum value of 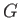 in Equation (9.59)
is achieved when all
in Equation (9.59)
is achieved when all 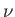 moles of the substance transform into phase 1, so that
moles of the substance transform into phase 1, so that
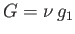 . In this case, phase 1 is the stable
one. On the other hand, if
. In this case, phase 1 is the stable
one. On the other hand, if 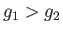 then the minimum value of
then the minimum value of 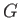 is achieved when all
is achieved when all 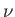 moles of the substance transform into phase 2, so that
moles of the substance transform into phase 2, so that
 . In this case, phase 2 is the stable
one. Finally, if
. In this case, phase 2 is the stable
one. Finally, if 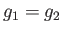 then the condition (9.59) is automatically satisfied, and any amount,
then the condition (9.59) is automatically satisfied, and any amount, 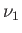 , of phase 1 can coexist with the
remaining amount,
, of phase 1 can coexist with the
remaining amount,
 , of phase 2. The locus of the points in the
, of phase 2. The locus of the points in the  -
- plane where
plane where 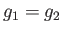 then
represents a phase-equilibrium line along which the two phases can coexist in equilibrium. This line
divides the
then
represents a phase-equilibrium line along which the two phases can coexist in equilibrium. This line
divides the  -
- plane into two regions. The first corresponds to
plane into two regions. The first corresponds to 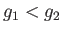 , so that phase 1 is stable. The
second corresponds to
, so that phase 1 is stable. The
second corresponds to 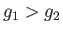 , so that phase 2 is stable. See Figure 9.1.
, so that phase 2 is stable. See Figure 9.1.



Next: Clausius-Clapeyron Equation
Up: Multi-Phase Systems
Previous: Stability of Single-Phase Substance
Richard Fitzpatrick
2016-01-25
![]() , of the system is a minimum:
, of the system is a minimum:

![]() is a well-defined function characteristic of phase 1. Likewise,
is a well-defined function characteristic of phase 1. Likewise, ![]() is a
well-defined function characteristic of phase 2. If
is a
well-defined function characteristic of phase 2. If ![]() and
and ![]() are such that
are such that ![]() then the minimum value of
then the minimum value of ![]() in Equation (9.59)
is achieved when all
in Equation (9.59)
is achieved when all ![]() moles of the substance transform into phase 1, so that
moles of the substance transform into phase 1, so that
![]() . In this case, phase 1 is the stable
one. On the other hand, if
. In this case, phase 1 is the stable
one. On the other hand, if ![]() then the minimum value of
then the minimum value of ![]() is achieved when all
is achieved when all ![]() moles of the substance transform into phase 2, so that
moles of the substance transform into phase 2, so that
![]() . In this case, phase 2 is the stable
one. Finally, if
. In this case, phase 2 is the stable
one. Finally, if ![]() then the condition (9.59) is automatically satisfied, and any amount,
then the condition (9.59) is automatically satisfied, and any amount, ![]() , of phase 1 can coexist with the
remaining amount,
, of phase 1 can coexist with the
remaining amount,
![]() , of phase 2. The locus of the points in the
, of phase 2. The locus of the points in the ![]() -
-![]() plane where
plane where ![]() then
represents a phase-equilibrium line along which the two phases can coexist in equilibrium. This line
divides the
then
represents a phase-equilibrium line along which the two phases can coexist in equilibrium. This line
divides the ![]() -
-![]() plane into two regions. The first corresponds to
plane into two regions. The first corresponds to ![]() , so that phase 1 is stable. The
second corresponds to
, so that phase 1 is stable. The
second corresponds to ![]() , so that phase 2 is stable. See Figure 9.1.
, so that phase 2 is stable. See Figure 9.1.