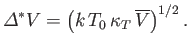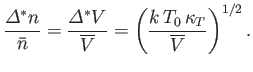Next: Equilibrium Between Phases
Up: Multi-Phase Systems
Previous: Equilibrium of Constant-Temperature Constant-Pressure
Stability of Single-Phase Substance
Consider a system in a single phase (e.g., a liquid or a solid). Let us focus attention on a small, but
macroscopic part,  , of this system. Here,
, of this system. Here,  consists of a fixed number of particles,
consists of a fixed number of particles, 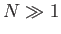 . The remainder of the system is,
relatively, very large, and, therefore, acts like a reservoir held at some constant temperature,
. The remainder of the system is,
relatively, very large, and, therefore, acts like a reservoir held at some constant temperature, 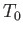 , and constant pressure,
, and constant pressure, 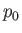 .
According to Equation (9.25), the condition for stable equilibrium, applied to
.
According to Equation (9.25), the condition for stable equilibrium, applied to  , is
, is
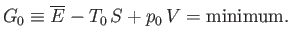 |
(9.30) |
Let the temperature,  , and the volume,
, and the volume,  , be the two independent parameters that specify the
macrostate of
, be the two independent parameters that specify the
macrostate of  . Consider, first, a situation where
. Consider, first, a situation where  is fixed, but
is fixed, but  is allowed to vary. Suppose that the minimum of
is allowed to vary. Suppose that the minimum of 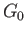 occurs for
occurs for
 , when
, when
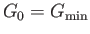 . Expanding
. Expanding 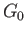 about its minimum, and writing
about its minimum, and writing
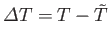 , we obtain
, we obtain
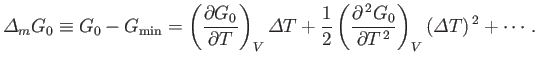 |
(9.31) |
Here, all derivatives are evaluated at
 . Because
. Because
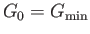 is a stationary point (i.e., a maximum or a minimum),
is a stationary point (i.e., a maximum or a minimum),
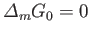 to first order in
to first order in
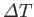 .
In other words,
.
In other words,
Furthermore, because 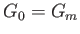 is a minimum, rather than a maximum,
is a minimum, rather than a maximum,
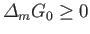 to second order in
to second order in
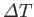 . In other words,
. In other words,
According to Equation (9.30), the condition, (9.32), that 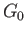 be stationary yields
be stationary yields
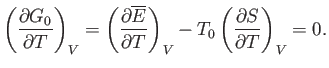 |
(9.34) |
However, the fundamental thermodynamic relation
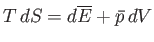 |
(9.35) |
implies that if  is fixed then
is fixed then
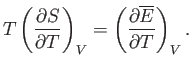 |
(9.36) |
Thus, Equation (9.34) becomes
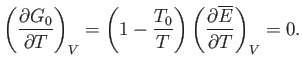 |
(9.37) |
Recalling that the derivatives are evaluated at
 , we get
, we get
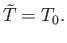 |
(9.38) |
Thus, we arrive at the rather obvious conclusion that a necessary condition for equilibrium is that the temperature of the subsystem  be the same as
that of the surrounding medium.
be the same as
that of the surrounding medium.
Equations (9.33) and (9.37) imply that
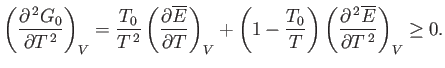 |
(9.39) |
Recalling that the derivatives are evaluated at
 , and that
, and that
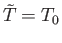 , the second term on the right-hand side of
the previous equation vanishes, and we obtain
, the second term on the right-hand side of
the previous equation vanishes, and we obtain
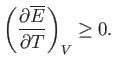 |
(9.40) |
However, this derivative is simply the heat capacity, 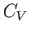 , at constant volume. Thus, we deduce that a fundamental
criterion for the stability of any phase is
, at constant volume. Thus, we deduce that a fundamental
criterion for the stability of any phase is
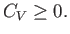 |
(9.41) |
The previous condition is a particular example of a very general rule, known as Le Chátelier's principle, which states that
If a system is in a stable equilibrium then any spontaneous change of its parameters must give rise to processes that tend to
restore the system to equilibrium.
To show how this principle applies to the present case, suppose that the temperature,  , of the subsystem
, of the subsystem  has increased
above that of its surroundings,
has increased
above that of its surroundings, 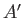 , as a result of a spontaneous fluctuation. The process brought into play is the spontaneous flow of heat
from system
, as a result of a spontaneous fluctuation. The process brought into play is the spontaneous flow of heat
from system  , at the higher temperature, to its surroundings
, at the higher temperature, to its surroundings 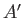 , which brings about a decrease in the energy,
, which brings about a decrease in the energy,
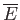 , of
, of  (i.e.,
(i.e.,
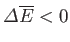 ). By Le Chátelier's principle, this energy decrease must act to decrease the temperature of
). By Le Chátelier's principle, this energy decrease must act to decrease the temperature of
 (i.e.,
(i.e.,
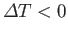 ), so as to restore
), so as to restore  to its equilibrium state (in which its temperature is the same as its surroundings). Hence, it follows that
to its equilibrium state (in which its temperature is the same as its surroundings). Hence, it follows that
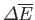 and
and
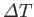 have the same sign, so
that
have the same sign, so
that
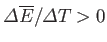 , in agreement with Equation (9.40).
, in agreement with Equation (9.40).
Suppose, now, that the temperature of subsystem  is fixed at
is fixed at 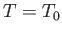 , but that its volume,
, but that its volume,  , is allowed to
vary. We can write
, is allowed to
vary. We can write
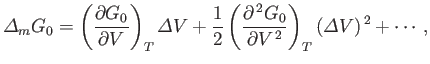 |
(9.42) |
where
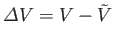 , and the expansion is about the volume
, and the expansion is about the volume
 at which
at which 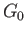 attains its
minimum value. The condition that
attains its
minimum value. The condition that 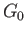 is stationary yields
is stationary yields
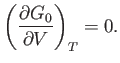 |
(9.43) |
The condition that the stationary point is a minimum gives
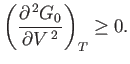 |
(9.44) |
Making use of Equation (9.30), we get
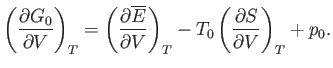 |
(9.45) |
However, Equation (9.35) implies that
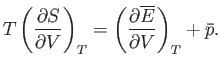 |
(9.46) |
Hence,
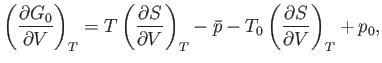 |
(9.47) |
or
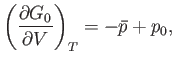 |
(9.48) |
because 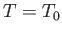 . Thus, the condition (9.43) yields
. Thus, the condition (9.43) yields
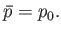 |
(9.49) |
This rather obvious result states that in equilibrium the pressure of subsystem  must be equal to that of the surrounding medium.
must be equal to that of the surrounding medium.
Equations (9.44) and (9.48) imply that
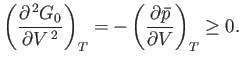 |
(9.50) |
When expressed in terms of the isothermal compressibility,
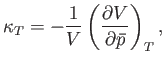 |
(9.51) |
the stability criterion (9.50) is equivalent to
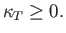 |
(9.52) |
To show how the preceding stability condition is consistent with Le Chátelier's principle, suppose that the volume of subsystem
 has increased by an amount
has increased by an amount
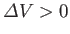 , as a result of a spontaneous fluctuation. The pressure,
, as a result of a spontaneous fluctuation. The pressure, 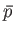 , of
, of  must then
decrease below that of its surroundings (i.e.,
must then
decrease below that of its surroundings (i.e.,
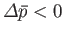 ) in order to ensure that the net force exerted on
) in order to ensure that the net force exerted on  by
its surroundings is such as to reduce the volume of
by
its surroundings is such as to reduce the volume of  back towards its equilibrium value. In other words,
back towards its equilibrium value. In other words,
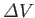 and
and
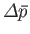 must have opposite signs, implying that
must have opposite signs, implying that
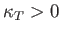 .
.
The preceding discussion allows us to characterize the spontaneous volume fluctuations of the small subsystem  . The
most probable situation is that where
. The
most probable situation is that where  takes the value
takes the value 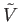 that minimizes
that minimizes 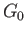 , so that
, so that
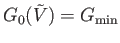 .
Let
.
Let 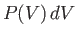 denote the probability that the volume of
denote the probability that the volume of  lies between
lies between  and
and 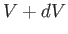 . According to Equation (9.29),
. According to Equation (9.29),
![$\displaystyle P(V) dV \propto \exp\left[-\frac{G_0(V)}{k T_0}\right] dV.$](img2697.png) |
(9.53) |
However, when
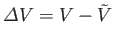 is small, the expansion (9.42) is applicable. By virtue of Equations (9.43), (9.50),
and (9.51), the expansion yields
is small, the expansion (9.42) is applicable. By virtue of Equations (9.43), (9.50),
and (9.51), the expansion yields
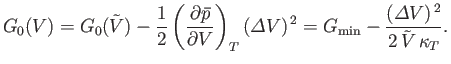 |
(9.54) |
Thus, Equation (9.53) becomes
![$\displaystyle P(V) dV =B\exp\left[-\frac{(V-\tilde{V})^{ 2}}{2 k T_0 \kappa_T \tilde{V}}\right]dV,$](img2699.png) |
(9.55) |
where we have absorbed
 into the constant of proportionality,
into the constant of proportionality, 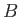 . Of course,
. Of course, 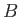 can be determined via the requirement that
the integral of
can be determined via the requirement that
the integral of 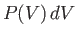 over all possible values of the volume,
over all possible values of the volume,  , be equal to unity.
, be equal to unity.
The probability distribution (9.55) is a Gaussian whose maximum lies at
 . Thus,
. Thus, 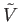 is equal to the
mean volume,
is equal to the
mean volume,
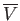 . Moreover, the standard deviation of the spontaneous fluctuations of
. Moreover, the standard deviation of the spontaneous fluctuations of  about its mean value is
about its mean value is
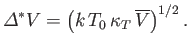 |
(9.56) |
(See Section 2.9.)
The fluctuations in  imply corresponding fluctuations in the number of particles per unit volume,
imply corresponding fluctuations in the number of particles per unit volume, 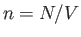 , (and, hence, in the mean
density) of the subsystem
, (and, hence, in the mean
density) of the subsystem  . The fluctuations in
. The fluctuations in 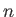 are centered on the mean value
are centered on the mean value
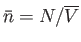 . For relatively
small fluctuations,
. For relatively
small fluctuations,
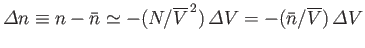 .
Hence,
.
Hence,
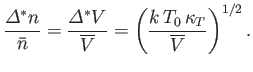 |
(9.57) |
Note that the relative magnitudes of the density and volume fluctuations are inversely proportional to the
square-root of the volume,
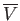 , under consideration.
, under consideration.
An interesting situation arises when
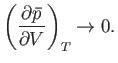 |
(9.58) |
In this limit,
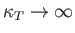 , and the density fluctuations become very large. [They do not, however, become infinite,
because the neglect of third-order, and higher, terms in the expansion (9.42) is no longer justified.]
The condition
, and the density fluctuations become very large. [They do not, however, become infinite,
because the neglect of third-order, and higher, terms in the expansion (9.42) is no longer justified.]
The condition
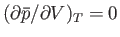 defines the so-called critical point of the substance, at which the
distinction between its liquid and gas phases disappears. (See Section 9.10.) The very large density fluctuations at the critical
point lead to strong scattering of light. As a result, a substance that is ordinarily transparent will assume a milky-white
appearance at its critical point (e.g.,
defines the so-called critical point of the substance, at which the
distinction between its liquid and gas phases disappears. (See Section 9.10.) The very large density fluctuations at the critical
point lead to strong scattering of light. As a result, a substance that is ordinarily transparent will assume a milky-white
appearance at its critical point (e.g.,
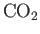 when it approaches its critical point at 304K and 73 atmospheres). This interesting
phenomenon is called critical-point opalecance.
when it approaches its critical point at 304K and 73 atmospheres). This interesting
phenomenon is called critical-point opalecance.



Next: Equilibrium Between Phases
Up: Multi-Phase Systems
Previous: Equilibrium of Constant-Temperature Constant-Pressure
Richard Fitzpatrick
2016-01-25
![]() , and the volume,
, and the volume, ![]() , be the two independent parameters that specify the
macrostate of
, be the two independent parameters that specify the
macrostate of ![]() . Consider, first, a situation where
. Consider, first, a situation where ![]() is fixed, but
is fixed, but ![]() is allowed to vary. Suppose that the minimum of
is allowed to vary. Suppose that the minimum of ![]() occurs for
occurs for
![]() , when
, when
![]() . Expanding
. Expanding ![]() about its minimum, and writing
about its minimum, and writing
![]() , we obtain
, we obtain
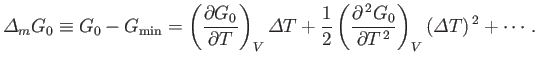
![]() be stationary yields
be stationary yields
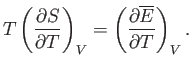
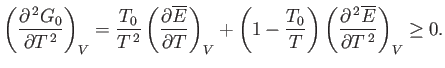
![]() is fixed at
is fixed at ![]() , but that its volume,
, but that its volume, ![]() , is allowed to
vary. We can write
, is allowed to
vary. We can write
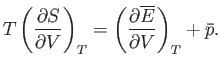
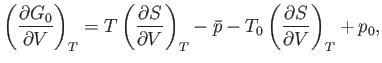
![]() has increased by an amount
has increased by an amount
![]() , as a result of a spontaneous fluctuation. The pressure,
, as a result of a spontaneous fluctuation. The pressure, ![]() , of
, of ![]() must then
decrease below that of its surroundings (i.e.,
must then
decrease below that of its surroundings (i.e.,
![]() ) in order to ensure that the net force exerted on
) in order to ensure that the net force exerted on ![]() by
its surroundings is such as to reduce the volume of
by
its surroundings is such as to reduce the volume of ![]() back towards its equilibrium value. In other words,
back towards its equilibrium value. In other words,
![]() and
and
![]() must have opposite signs, implying that
must have opposite signs, implying that
![]() .
.
![]() . The
most probable situation is that where
. The
most probable situation is that where ![]() takes the value
takes the value ![]() that minimizes
that minimizes ![]() , so that
, so that
![]() .
Let
.
Let ![]() denote the probability that the volume of
denote the probability that the volume of ![]() lies between
lies between ![]() and
and ![]() . According to Equation (9.29),
. According to Equation (9.29),
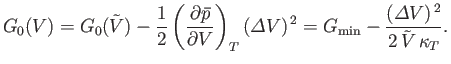
![]() . Thus,
. Thus, ![]() is equal to the
mean volume,
is equal to the
mean volume,
![]() . Moreover, the standard deviation of the spontaneous fluctuations of
. Moreover, the standard deviation of the spontaneous fluctuations of ![]() about its mean value is
about its mean value is