


Next: Equilibrium of Constant-Temperature System
Up: Multi-Phase Systems
Previous: Introduction
Consider a thermally isolated system,  . According to Section 5.6, any spontaneously occurring
process is such that the system's entropy tends to increase in time. In statistical terms, this
means that the system evolves toward a situation of greater intrinsic probability. Thus, in any
spontaneous process, the change in entropy satisfies
. According to Section 5.6, any spontaneously occurring
process is such that the system's entropy tends to increase in time. In statistical terms, this
means that the system evolves toward a situation of greater intrinsic probability. Thus, in any
spontaneous process, the change in entropy satisfies
 |
(9.1) |
It follows that if a stable equilibrium state has been attained [i.e., one in which no further spontaneous processes (other than
random fluctuations) can take place] then this state is such that 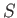 is maximized. In other words, it is the most
probable state of the system, subject to the given constraints. Thus, we can make the following statement:
is maximized. In other words, it is the most
probable state of the system, subject to the given constraints. Thus, we can make the following statement:
For a thermally isolated system, the stable equilibrium state is such that
Now, in a thermally isolated system, the first law of thermodynamics implies that
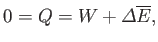 |
(9.2) |
or
 |
(9.3) |
If the external parameters of the system (e.g., its volume) are kept fixed, so that no work is done (i.e., 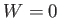 ), then
), then
 |
(9.4) |
as 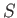 evolves toward its maximum value.
evolves toward its maximum value.
We can phrase the previous argument in more explicit statistical terms. Suppose that an
isolated system is described by a parameter  (or by several such parameters), but that its total
energy is constant. Let
(or by several such parameters), but that its total
energy is constant. Let
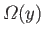 denote the number of microstates accessible to the system
when this parameter lies between
denote the number of microstates accessible to the system
when this parameter lies between  and
and
 (
(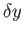 being some fixed small interval).
The corresponding entropy of the system is
being some fixed small interval).
The corresponding entropy of the system is
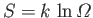 . (See Section 5.6.) If the parameter
. (See Section 5.6.) If the parameter  is free to vary then
the principle of equal a priori probabilities asserts that, in an equilibrium state, the probability,
is free to vary then
the principle of equal a priori probabilities asserts that, in an equilibrium state, the probability,  , of
finding the system with the parameter between
, of
finding the system with the parameter between  and
and
 is given by
is given by
![$\displaystyle P(y)\propto {\mit\Omega} (y)= \exp\left[\frac{S(y)}{k}\right].$](img2602.png) |
(9.5) |
(See Section 3.3.)
The previous expression shows explicitly that the most probable state is one in which 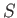 attains a maximum value, and
also allows us to determine the relative probability of fluctuations about this state.
attains a maximum value, and
also allows us to determine the relative probability of fluctuations about this state.



Next: Equilibrium of Constant-Temperature System
Up: Multi-Phase Systems
Previous: Introduction
Richard Fitzpatrick
2016-01-25
![]() (or by several such parameters), but that its total
energy is constant. Let
(or by several such parameters), but that its total
energy is constant. Let
![]() denote the number of microstates accessible to the system
when this parameter lies between
denote the number of microstates accessible to the system
when this parameter lies between ![]() and
and
![]() (
(![]() being some fixed small interval).
The corresponding entropy of the system is
being some fixed small interval).
The corresponding entropy of the system is
![]() . (See Section 5.6.) If the parameter
. (See Section 5.6.) If the parameter ![]() is free to vary then
the principle of equal a priori probabilities asserts that, in an equilibrium state, the probability,
is free to vary then
the principle of equal a priori probabilities asserts that, in an equilibrium state, the probability, ![]() , of
finding the system with the parameter between
, of
finding the system with the parameter between ![]() and
and
![]() is given by
is given by