


Next: Equilibrium of Constant-Temperature Constant-Pressure
Up: Multi-Phase Systems
Previous: Equilibrium of Isolated System
A knowledge of the equilibrium conditions for an isolated system permits us to deduce similar conditions for
other situations of physical interest. For instance, much experimental work is performed under conditions of
constant temperature. Thus, it would be interesting to investigate the equilibrium of some system,  , in thermal
contact with a heat reservoir,
, in thermal
contact with a heat reservoir,  , that is held at the constant absolute temperature
, that is held at the constant absolute temperature 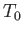 .
.
The combined system, 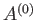 , consisting of the system
, consisting of the system  and the heat reservoir
and the heat reservoir  , is an isolated system of the type
discussed in the previous section. The entropy,
, is an isolated system of the type
discussed in the previous section. The entropy, 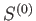 , of
, of 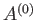 therefore satisfies condition (9.1). In other
words, in any spontaneous process,
therefore satisfies condition (9.1). In other
words, in any spontaneous process,
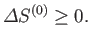 |
(9.6) |
However, this condition can also be expressed in terms of quantities that only refer to the system  . In fact,
. In fact,
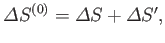 |
(9.7) |
where
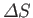 is the entropy change of
is the entropy change of  , and
, and
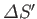 that of the reservoir. But, if
that of the reservoir. But, if  absorbs heat
absorbs heat 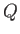 from the reservoir
from the reservoir  during the process then
during the process then  absorbs heat
absorbs heat 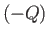 , and suffers a
corresponding entropy change
, and suffers a
corresponding entropy change
 |
(9.8) |
(because it remains in equilibrium at the constant temperature 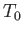 ). Furthermore, the first law of thermodynamics implies that
). Furthermore, the first law of thermodynamics implies that
 |
(9.9) |
where
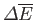 is the change in internal energy of
is the change in internal energy of  , and
, and 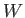 is the work done by
is the work done by  . Thus,
Equation (9.7) can be written
. Thus,
Equation (9.7) can be written
 |
(9.10) |
or
 |
(9.11) |
where use has been made of the fact that 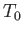 is a constant. Here,
is a constant. Here,
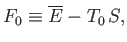 |
(9.12) |
reduces to the Helmholtz free energy,
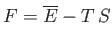 , of system
, of system  , when the latter has a temperature,
, when the latter has a temperature,  , equal to that of the
heat reservoir,
, equal to that of the
heat reservoir,  . Of course, in the general case in which
. Of course, in the general case in which  is not in equilibrium with
is not in equilibrium with  , the former system's temperature is
not necessarily equal to
, the former system's temperature is
not necessarily equal to 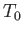 .
.
The fundamental condition (9.6) can be combined with Equation (9.11) to give
 |
(9.13) |
(assuming that 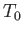 is positive, as is normally the case). This relation implies that the maximum work that
can be done by a system in contact with a heat reservoir is
is positive, as is normally the case). This relation implies that the maximum work that
can be done by a system in contact with a heat reservoir is
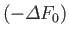 . (Incidentally, this is the reason for the name
``free energy'' given to
. (Incidentally, this is the reason for the name
``free energy'' given to  .) The maximum work corresponds to the equality sign in the preceding equation, and
is obtained when the process used is quasi-static (so that
.) The maximum work corresponds to the equality sign in the preceding equation, and
is obtained when the process used is quasi-static (so that  is always in equilibrium with
is always in equilibrium with  , and
, and 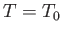 ).
Equation (9.13) should be compared to the rather different relation (9.3) that pertains to an isolated system.
).
Equation (9.13) should be compared to the rather different relation (9.3) that pertains to an isolated system.
If the external parameters of system  are held constant then
are held constant then 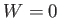 , and Equation (9.13) yields the condition
, and Equation (9.13) yields the condition
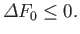 |
(9.14) |
This equation is analogous to Equation (9.1) for an isolated system. It implies that if a system is in thermal contact with a heat reservoir then
its Helmholtz free energy tends to decrease. Thus, we arrive at the following statement:
If a system, whose external parameters are fixed, is in thermal contact with a heat reservoir then the stable equilibrium state
is such that
The preceding statement can again be phrased in more explicit statistical terms. Suppose that the external parameters of  are fixed, so that
are fixed, so that
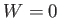 . Furthermore, let
. Furthermore, let  be described by some parameter
be described by some parameter  . The thermodynamic functions of
. The thermodynamic functions of  --namely,
--namely, 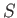 and
and
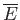 --have the
definite values
--have the
definite values 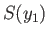 and
and
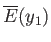 , respectively, when
, respectively, when  has a given value
has a given value 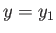 . If the parameter changes to some other value,
. If the parameter changes to some other value,  ,
then these functions change by the corresponding amounts
,
then these functions change by the corresponding amounts
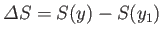 and
and
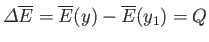 .
The entropy of the heat reservoir,
.
The entropy of the heat reservoir,  , also changes because it absorbs heat. The corresponding change in the total entropy of
, also changes because it absorbs heat. The corresponding change in the total entropy of 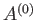 is given by
Equation (9.11) (with
is given by
Equation (9.11) (with 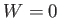 ):
):
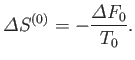 |
(9.15) |
But, in an equilibrium state, the probability,  , that the parameter lies between
, that the parameter lies between  and
and
 is proportional to the number of states,
is proportional to the number of states,
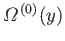 , accessible to the isolated total system,
, accessible to the isolated total system, 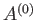 , when the parameter lies in this range. Thus, by analogy with Equation (9.5),
we have
, when the parameter lies in this range. Thus, by analogy with Equation (9.5),
we have
![$\displaystyle P(y)\propto {\mit\Omega}^{ (0)}(y) = \exp\left[\frac{S^{(0)}(y)}{k}\right].$](img2627.png) |
(9.16) |
However, from Equation (9.15),
![$\displaystyle S^{(0)}(y) = S^{(0)}(y_1)-\frac{{\mit\Delta}F_0}{T_0} = S^{(0)}(y_1) - \left[\frac{F_0(y)-F_0(y_1)}{T_0}\right].$](img2628.png) |
(9.17) |
Now, because 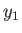 is just some arbitrary constant, the corresponding constant terms can be absorbed into the constant of
proportionality in Equation (9.16), which then becomes
is just some arbitrary constant, the corresponding constant terms can be absorbed into the constant of
proportionality in Equation (9.16), which then becomes
![$\displaystyle P(y)\propto \exp\left[-\frac{F_0(y)}{k T_0}\right].$](img2630.png) |
(9.18) |
This equation shows explicitly that the most probable state is one in which 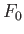 attains a minimum value, and also allows us to determine the relative probability of fluctuations about this state.
attains a minimum value, and also allows us to determine the relative probability of fluctuations about this state.



Next: Equilibrium of Constant-Temperature Constant-Pressure
Up: Multi-Phase Systems
Previous: Equilibrium of Isolated System
Richard Fitzpatrick
2016-01-25
![]() , consisting of the system
, consisting of the system ![]() and the heat reservoir
and the heat reservoir ![]() , is an isolated system of the type
discussed in the previous section. The entropy,
, is an isolated system of the type
discussed in the previous section. The entropy, ![]() , of
, of ![]() therefore satisfies condition (9.1). In other
words, in any spontaneous process,
therefore satisfies condition (9.1). In other
words, in any spontaneous process,


![]() are held constant then
are held constant then ![]() , and Equation (9.13) yields the condition
, and Equation (9.13) yields the condition
![]() are fixed, so that
are fixed, so that
![]() . Furthermore, let
. Furthermore, let ![]() be described by some parameter
be described by some parameter ![]() . The thermodynamic functions of
. The thermodynamic functions of ![]() --namely,
--namely, ![]() and
and
![]() --have the
definite values
--have the
definite values ![]() and
and
![]() , respectively, when
, respectively, when ![]() has a given value
has a given value ![]() . If the parameter changes to some other value,
. If the parameter changes to some other value, ![]() ,
then these functions change by the corresponding amounts
,
then these functions change by the corresponding amounts
![]() and
and
![]() .
The entropy of the heat reservoir,
.
The entropy of the heat reservoir, ![]() , also changes because it absorbs heat. The corresponding change in the total entropy of
, also changes because it absorbs heat. The corresponding change in the total entropy of ![]() is given by
Equation (9.11) (with
is given by
Equation (9.11) (with ![]() ):
):
![$\displaystyle S^{(0)}(y) = S^{(0)}(y_1)-\frac{{\mit\Delta}F_0}{T_0} = S^{(0)}(y_1) - \left[\frac{F_0(y)-F_0(y_1)}{T_0}\right].$](img2628.png)
![$\displaystyle P(y)\propto \exp\left[-\frac{F_0(y)}{k T_0}\right].$](img2630.png)