


Next: Representation of Angular Momentum
Up: Orbital Angular Momentum
Previous: Introduction
Angular Momentum Operators
In classical mechanics, the vector angular momentum, L, of a particle of
position vector 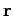 and linear momentum
and linear momentum
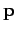 is defined as
is defined as
 |
(526) |
It follows that
Let us, first of all, consider whether it is possible to use the above expressions as the
definitions of the operators corresponding to the components of angular
momentum in quantum mechanics, assuming that the 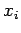 and
and  (where
(where 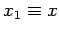 ,
, 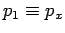 ,
, 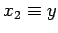 , etc.)
correspond to the appropriate quantum mechanical position and momentum operators. The first point to note is that expressions (527)-(529) are unambiguous with respect to the order of the terms in multiplicative factors, since the various position and momentum operators
appearing in them all commute
with one another [see Eqs. (483)]. Moreover, given that the
, etc.)
correspond to the appropriate quantum mechanical position and momentum operators. The first point to note is that expressions (527)-(529) are unambiguous with respect to the order of the terms in multiplicative factors, since the various position and momentum operators
appearing in them all commute
with one another [see Eqs. (483)]. Moreover, given that the 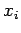 and
the
and
the  are Hermitian operators, it is easily seen that the
are Hermitian operators, it is easily seen that the 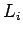 are
also Hermitian. This is important, since only Hermitian operators can represent physical variables in quantum mechanics (see Sect. 4.6).
We, thus, conclude that Eqs. (527)-(529) are plausible
definitions for the quantum mechanical operators which represent the components of angular momentum.
are
also Hermitian. This is important, since only Hermitian operators can represent physical variables in quantum mechanics (see Sect. 4.6).
We, thus, conclude that Eqs. (527)-(529) are plausible
definitions for the quantum mechanical operators which represent the components of angular momentum.
Let us now derive the commutation relations for the 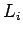 .
For instance,
.
For instance,
where use has been made of the definitions of the 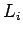 [see Eqs. (527)-(529)], and commutation relations (481)-(483)
for the
[see Eqs. (527)-(529)], and commutation relations (481)-(483)
for the 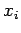 and
and  . There are two similar commutation relations:
one for
. There are two similar commutation relations:
one for 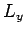 and
and 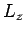 , and one for
, and one for 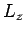 and
and 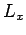 . Collecting all of these
commutation relations together, we obtain
. Collecting all of these
commutation relations together, we obtain
By analogy with classical mechanics, the operator 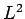 , which represents
the magnitude squared of the angular momentum vector, is defined
, which represents
the magnitude squared of the angular momentum vector, is defined
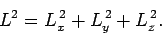 |
(534) |
Now, it is easily demonstrated that if  and
and  are two general
operators then
are two general
operators then
![\begin{displaymath}[A^2,B]= A [A, B] +[A,B] A.
\end{displaymath}](img1326.png) |
(535) |
Hence,
where use has been made of Eqs. (531)-(533). In other words,
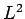 commutes with
commutes with 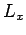 . Likewise, it is easily demonstrated that
. Likewise, it is easily demonstrated that
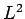 also commutes with
also commutes with 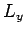 , and with
, and with 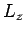 . Thus,
. Thus,
![\begin{displaymath}[L^2, L_x]= [L^2, L_y] = [L^2,L_z] = 0.
\end{displaymath}](img1331.png) |
(537) |
Recall, from Sect. 4.10, that in order for two physical quantities
to be (exactly) measured simultaneously, the operators which represent
them in quantum mechanics must commute with one another. Hence,
the commutation relations (531)-(533) and (537)
imply that we can only simultaneously measure the magnitude squared of
the angular momentum vector, 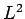 , together with, at most, one of its
Cartesian components. By convention, we shall always choose to measure
the
, together with, at most, one of its
Cartesian components. By convention, we shall always choose to measure
the 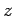 -component,
-component, 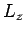 .
.
Finally, it is helpful to define the operators
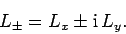 |
(538) |
Note that 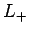 and
and 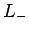 are not Hermitian operators, but are
the Hermitian conjugates of one another (see Sect. 4.6): i.e.,
are not Hermitian operators, but are
the Hermitian conjugates of one another (see Sect. 4.6): i.e.,
![\begin{displaymath}
(L_\pm)^\dag = L_\mp,\ [0.5ex]
\end{displaymath}](img1335.png) |
(539) |
Moreover, it is easily seen that
Likewise,
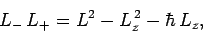 |
(541) |
giving
![\begin{displaymath}[L_+, L_-]= 2 \hbar L_z.
\end{displaymath}](img1340.png) |
(542) |
We also have
and, similarly,
![\begin{displaymath}[L_-,L_z]= \hbar L_-.
\end{displaymath}](img1343.png) |
(544) |



Next: Representation of Angular Momentum
Up: Orbital Angular Momentum
Previous: Introduction
Richard Fitzpatrick
2010-07-20
![]() .
For instance,
.
For instance,
![]() , which represents
the magnitude squared of the angular momentum vector, is defined
, which represents
the magnitude squared of the angular momentum vector, is defined
![]() , together with, at most, one of its
Cartesian components. By convention, we shall always choose to measure
the
, together with, at most, one of its
Cartesian components. By convention, we shall always choose to measure
the ![]() -component,
-component, ![]() .
.