


Next: Continuous Eigenvalues
Up: Fundamentals of Quantum Mechanics
Previous: Eigenstates and Eigenvalues
Measurement
Suppose that  is an Hermitian operator corresponding to some dynamical
variable. By analogy with the discussion in Sect. 3.16, we expect that if a measurement of
is an Hermitian operator corresponding to some dynamical
variable. By analogy with the discussion in Sect. 3.16, we expect that if a measurement of  yields the result
yields the result 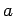 then the act of measurement will cause the wavefunction to collapse to a state in which a measurement
of
then the act of measurement will cause the wavefunction to collapse to a state in which a measurement
of  is bound to give the result
is bound to give the result 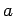 .
What sort of wavefunction,
.
What sort of wavefunction,  , is such that a measurement of
, is such that a measurement of  is
bound to yield a certain result,
is
bound to yield a certain result, 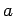 ? Well, expressing
? Well, expressing  as
a linear combination of the eigenstates of
as
a linear combination of the eigenstates of  , we have
, we have
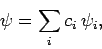 |
(266) |
where 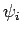 is an eigenstate of
is an eigenstate of  corresponding to the eigenvalue
corresponding to the eigenvalue 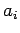 . If a measurement of
. If a measurement of  is bound to yield the result
is bound to yield the result 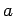 then
then
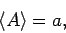 |
(267) |
and
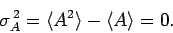 |
(268) |
Now it is easily seen that
Thus, Eq. (268) gives
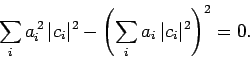 |
(271) |
Furthermore, the normalization condition yields
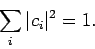 |
(272) |
For instance, suppose that there are only two eigenstates. The above two
equations then reduce to  , and
, and  , where
, where 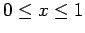 ,
and
,
and
 |
(273) |
The only solutions are 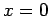 and
and 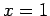 . This result can easily
be generalized to the case where there are more than two eigenstates.
It follows that a state associated with a definite value of
. This result can easily
be generalized to the case where there are more than two eigenstates.
It follows that a state associated with a definite value of  is
one in which one of the
is
one in which one of the 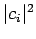 is unity, and all of the others are zero.
In other words, the only states associated with definite values of
is unity, and all of the others are zero.
In other words, the only states associated with definite values of  are the eigenstates of
are the eigenstates of  . It immediately
follows that the result of a measurement of
. It immediately
follows that the result of a measurement of  must be one of the eigenvalues of
must be one of the eigenvalues of  . Moreover, if a general wavefunction is expanded
as a linear combination of the eigenstates of
. Moreover, if a general wavefunction is expanded
as a linear combination of the eigenstates of  , like in Eq. (266),
then it is clear from Eq. (269), and the general definition of a mean,
that the probability of a measurement of
, like in Eq. (266),
then it is clear from Eq. (269), and the general definition of a mean,
that the probability of a measurement of  yielding the eigenvalue
yielding the eigenvalue 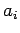 is simply
is simply 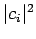 , where
, where 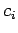 is the coefficient in front of
the
is the coefficient in front of
the 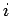 th eigenstate in the expansion. Note, from Eq. (272),
that these probabilities are properly normalized: i.e., the probability
of a measurement of
th eigenstate in the expansion. Note, from Eq. (272),
that these probabilities are properly normalized: i.e., the probability
of a measurement of  resulting in any possible answer is unity.
Finally, if a measurement of
resulting in any possible answer is unity.
Finally, if a measurement of  results in the eigenvalue
results in the eigenvalue 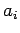 then
immediately after the measurement the system will be left in the
eigenstate corresponding to
then
immediately after the measurement the system will be left in the
eigenstate corresponding to 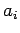 .
.
Consider two physical dynamical variables represented by the two
Hermitian operators  and
and  . Under what circumstances is
it possible to simultaneously measure these two variables (exactly)?
Well, the possible results of measurements of
. Under what circumstances is
it possible to simultaneously measure these two variables (exactly)?
Well, the possible results of measurements of  and
and  are the eigenvalues
of
are the eigenvalues
of  and
and  , respectively. Thus, to simultaneously measure
, respectively. Thus, to simultaneously measure  and
and  (exactly) there
must exist states which are simultaneous eigenstates of
(exactly) there
must exist states which are simultaneous eigenstates of  and
and  .
In fact, in order for
.
In fact, in order for  and
and  to be simultaneously measurable under all
circumstances, we need all of the eigenstates of
to be simultaneously measurable under all
circumstances, we need all of the eigenstates of  to also be eigenstates of
to also be eigenstates of  , and vice versa, so that all states associated with unique values of
, and vice versa, so that all states associated with unique values of  are
also associated with unique values of
are
also associated with unique values of  , and vice versa.
, and vice versa.
Now, we have already seen, in Sect. 4.8, that if  and
and  do not commute (i.e., if
do not commute (i.e., if  ) then they cannot
be simultaneously measured. This suggests that the condition
for simultaneous measurement is that
) then they cannot
be simultaneously measured. This suggests that the condition
for simultaneous measurement is that  and
and  should commute.
Suppose that this is the case, and that the
should commute.
Suppose that this is the case, and that the 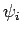 and
and 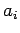 are the normalized eigenstates and
eigenvalues of
are the normalized eigenstates and
eigenvalues of  , respectively. It follows that
, respectively. It follows that
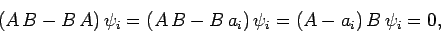 |
(274) |
or
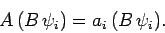 |
(275) |
Thus, 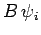 is an eigenstate of
is an eigenstate of  corresponding to
the eigenvalue
corresponding to
the eigenvalue 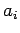 (though not necessarily a normalized one). In other words,
(though not necessarily a normalized one). In other words,
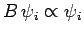 , or
, or
 |
(276) |
where 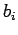 is a constant of proportionality.
Hence,
is a constant of proportionality.
Hence, 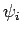 is an eigenstate of
is an eigenstate of  , and, thus, a simultaneous
eigenstate of
, and, thus, a simultaneous
eigenstate of  and
and  . We conclude that if
. We conclude that if  and
and  commute then
they possess simultaneous eigenstates, and are thus simultaneously measurable (exactly).
commute then
they possess simultaneous eigenstates, and are thus simultaneously measurable (exactly).



Next: Continuous Eigenvalues
Up: Fundamentals of Quantum Mechanics
Previous: Eigenstates and Eigenvalues
Richard Fitzpatrick
2010-07-20
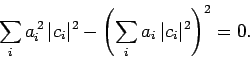
![]() , and
, and ![]() , where
, where ![]() ,
and
,
and
![]() and
and ![]() . Under what circumstances is
it possible to simultaneously measure these two variables (exactly)?
Well, the possible results of measurements of
. Under what circumstances is
it possible to simultaneously measure these two variables (exactly)?
Well, the possible results of measurements of ![]() and
and ![]() are the eigenvalues
of
are the eigenvalues
of ![]() and
and ![]() , respectively. Thus, to simultaneously measure
, respectively. Thus, to simultaneously measure ![]() and
and ![]() (exactly) there
must exist states which are simultaneous eigenstates of
(exactly) there
must exist states which are simultaneous eigenstates of ![]() and
and ![]() .
In fact, in order for
.
In fact, in order for ![]() and
and ![]() to be simultaneously measurable under all
circumstances, we need all of the eigenstates of
to be simultaneously measurable under all
circumstances, we need all of the eigenstates of ![]() to also be eigenstates of
to also be eigenstates of ![]() , and vice versa, so that all states associated with unique values of
, and vice versa, so that all states associated with unique values of ![]() are
also associated with unique values of
are
also associated with unique values of ![]() , and vice versa.
, and vice versa.
![]() and
and ![]() do not commute (i.e., if
do not commute (i.e., if ![]() ) then they cannot
be simultaneously measured. This suggests that the condition
for simultaneous measurement is that
) then they cannot
be simultaneously measured. This suggests that the condition
for simultaneous measurement is that ![]() and
and ![]() should commute.
Suppose that this is the case, and that the
should commute.
Suppose that this is the case, and that the ![]() and
and ![]() are the normalized eigenstates and
eigenvalues of
are the normalized eigenstates and
eigenvalues of ![]() , respectively. It follows that
, respectively. It follows that