


Next: Heisenberg's Uncertainty Principle
Up: Fundamentals of Quantum Mechanics
Previous: Operators
Fourier's theorerm (see Sect. 3.12), applied to one-dimensional wavefunctions, yields
where  represents wavenumber. However,
represents wavenumber. However, 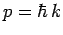 . Hence,
we can also write
. Hence,
we can also write
where
 is the momentum-space
equivalent to the real-space wavefunction
is the momentum-space
equivalent to the real-space wavefunction 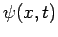 .
.
At this stage, it is convenient to introduce a useful function called the
Dirac delta-function. This function, denoted  , was
first devised by Paul Dirac, and has the following rather
unusual properties:
, was
first devised by Paul Dirac, and has the following rather
unusual properties:  is zero for
is zero for 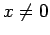 , and is infinite
at
, and is infinite
at 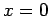 . However, the singularity at
. However, the singularity at 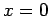 is such that
is such that
 |
(204) |
The delta-function is an example of what is known as a generalized function: i.e.,
its value is not well-defined at all  , but its integral is well-defined.
Consider the integral
, but its integral is well-defined.
Consider the integral
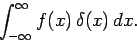 |
(205) |
Since  is only non-zero infinitesimally close to
is only non-zero infinitesimally close to 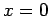 , we
can safely replace
, we
can safely replace 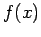 by
by 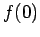 in the above integral (assuming
in the above integral (assuming 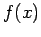 is well behaved at
is well behaved at 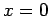 ), to give
), to give
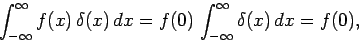 |
(206) |
where use has been made of Eq. (204). A simple generalization of this result yields
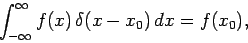 |
(207) |
which can also be thought of as an alternative definition of a delta-function.
Suppose that
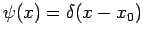 . It follows from Eqs. (203)
and (207) that
. It follows from Eqs. (203)
and (207) that
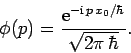 |
(208) |
Hence, Eq. (202) yields the important result
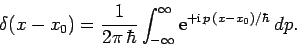 |
(209) |
Similarly,
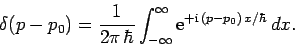 |
(210) |
It turns out that we can just as well formulate quantum mechanics using
momentum-space wavefunctions, 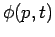 , as real-space wavefunctions,
, as real-space wavefunctions, 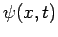 . The former scheme is known as the momentum representation of quantum mechanics. In the momentum representation,
wavefunctions are the Fourier transforms of the equivalent real-space
wavefunctions, and dynamical variables are represented by different operators. Furthermore, by analogy with Eq. (192), the
expectation value of some operator
. The former scheme is known as the momentum representation of quantum mechanics. In the momentum representation,
wavefunctions are the Fourier transforms of the equivalent real-space
wavefunctions, and dynamical variables are represented by different operators. Furthermore, by analogy with Eq. (192), the
expectation value of some operator 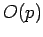 takes the form
takes the form
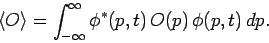 |
(211) |
Consider momentum. We can write
where use has been made of Eq. (202).
However, it follows from Eq. (210)
that
 |
(213) |
Hence, using Eq. (207), we obtain
 |
(214) |
Evidently, momentum is represented by the operator 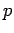 in the momentum
representation. The above expression also strongly suggests [by comparison with Eq. (158)] that
in the momentum
representation. The above expression also strongly suggests [by comparison with Eq. (158)] that
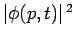 can be interpreted as
the probability density of a measurement of momentum yielding the
value
can be interpreted as
the probability density of a measurement of momentum yielding the
value 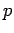 at time
at time  . It follows that
. It follows that 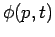 must satisfy an analogous normalization
condition to Eq. (140): i.e.,
must satisfy an analogous normalization
condition to Eq. (140): i.e.,
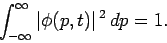 |
(215) |
Consider displacement. We can write
Integration by parts yields
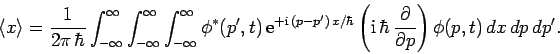 |
(217) |
Hence, making use of Eqs. (210) and (207), we obtain
 |
(218) |
Evidently, displacement is represented by the operator
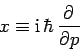 |
(219) |
in the momentum representation.
Finally, let us consider the normalization of the momentum-space wavefunction 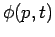 . We have
. We have
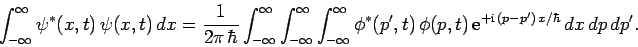 |
(220) |
Thus, it follows from Eqs. (207) and (210)
that
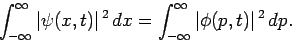 |
(221) |
Hence, if 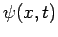 is properly normalized [see Eq. (140)] then
is properly normalized [see Eq. (140)] then 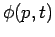 ,
as defined in Eq. (203), is also properly normalized [see Eq. (215)].
,
as defined in Eq. (203), is also properly normalized [see Eq. (215)].
The existence of the momentum representation illustrates an important point:
i.e., that there are many different, but entirely equivalent, ways
of mathematically formulating quantum mechanics. For instance, it
is also possible to represent wavefunctions as row and column vectors, and dynamical
variables
as matrices which act upon these vectors.



Next: Heisenberg's Uncertainty Principle
Up: Fundamentals of Quantum Mechanics
Previous: Operators
Richard Fitzpatrick
2010-07-20
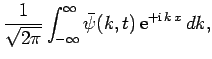
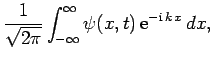
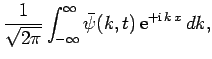
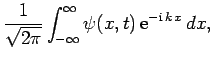
![]() , was
first devised by Paul Dirac, and has the following rather
unusual properties:
, was
first devised by Paul Dirac, and has the following rather
unusual properties: ![]() is zero for
is zero for ![]() , and is infinite
at
, and is infinite
at ![]() . However, the singularity at
. However, the singularity at ![]() is such that
is such that
![]() . It follows from Eqs. (203)
and (207) that
. It follows from Eqs. (203)
and (207) that
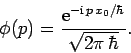
![]() , as real-space wavefunctions,
, as real-space wavefunctions, ![]() . The former scheme is known as the momentum representation of quantum mechanics. In the momentum representation,
wavefunctions are the Fourier transforms of the equivalent real-space
wavefunctions, and dynamical variables are represented by different operators. Furthermore, by analogy with Eq. (192), the
expectation value of some operator
. The former scheme is known as the momentum representation of quantum mechanics. In the momentum representation,
wavefunctions are the Fourier transforms of the equivalent real-space
wavefunctions, and dynamical variables are represented by different operators. Furthermore, by analogy with Eq. (192), the
expectation value of some operator ![]() takes the form
takes the form
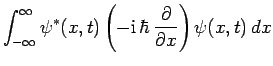
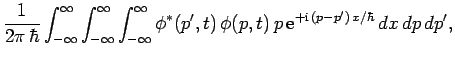
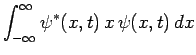
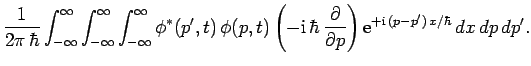
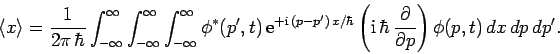
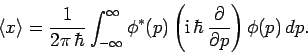
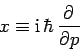
![]() . We have
. We have