


Next: Harmonic Perturbations
Up: Time-Dependent Perturbation Theory
Previous: Sudden Perturbations
Energy-Shifts and Decay-Widths
We have examined how a state 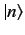 , other than the initial
state
, other than the initial
state 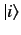 , becomes populated as a result of some time-dependent
perturbation applied to the system. Let us now consider
how the initial state becomes depopulated.
, becomes populated as a result of some time-dependent
perturbation applied to the system. Let us now consider
how the initial state becomes depopulated.
In this case, it is convenient to gradually turn on the perturbation from zero at
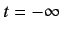 . Thus,
. Thus,
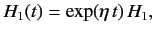 |
(821) |
where  is small and positive, and
is small and positive, and 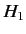 is a constant.
is a constant.
In the remote past,
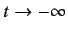 , the system is assumed to
be in the initial state
, the system is assumed to
be in the initial state 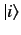 . Thus,
. Thus,
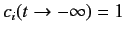 ,
and
,
and
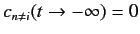 . Basically, we want to
calculate the time evolution of the coefficient
. Basically, we want to
calculate the time evolution of the coefficient 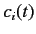 .
First, however, let us check that our previous Fermi golden rule result
still applies when the perturbing potential is turned on slowly,
instead of very suddenly. For
.
First, however, let us check that our previous Fermi golden rule result
still applies when the perturbing potential is turned on slowly,
instead of very suddenly. For
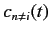 we have from Equations (795)-(796) that
we have from Equations (795)-(796) that
where
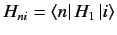 .
It follows that, to first order, the transition probability from state
.
It follows that, to first order, the transition probability from state 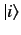 to state
to state 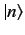 is
is
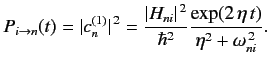 |
(824) |
The transition rate is given by
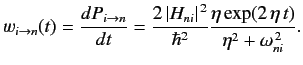 |
(825) |
Consider the limit
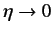 . In this limit,
. In this limit,
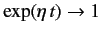 , but
, but
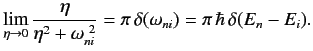 |
(826) |
Thus, Equation (825) yields the standard Fermi golden rule result
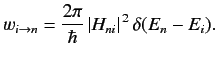 |
(827) |
It is clear that the delta-function in the above formula actually represents
a function that is highly peaked at some particular energy. The width
of the peak is determined by how fast the perturbation is switched on.
Let us now calculate 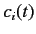 using Equations (795)-(797). We have
using Equations (795)-(797). We have
Thus, to second order we have
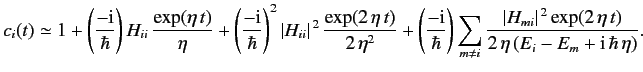 |
(831) |
Let us now consider the ratio
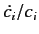 , where
, where
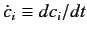 . Using Equation (831), we can evaluate this ratio in the limit
. Using Equation (831), we can evaluate this ratio in the limit
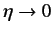 . We obtain
. We obtain
This result is formally correct to second order in perturbed quantities.
Note that the right-hand side of Equation (832) is independent of time.
We can write
 |
(833) |
where
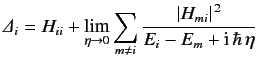 |
(834) |
is a constant.
According to a well-known result in pure mathematics,
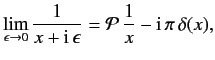 |
(835) |
where
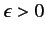 , and
, and 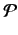 denotes the principal part.
It follows that
denotes the principal part.
It follows that
 |
(836) |
It is convenient to normalize the solution of
Equation (833) such that
 . Thus, we obtain
. Thus, we obtain
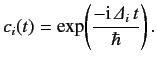 |
(837) |
According to Equation (744), the time evolution of the initial
state ket 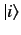 is given by
is given by
![$\displaystyle \vert i, t\rangle = \exp[-{\rm i}\,({\mit\Delta}_i + E_i)\,t/\hbar] \,\vert i\rangle.$](img1978.png) |
(838) |
We can rewrite this result as
![$\displaystyle \vert i, t\rangle = \exp(-{\rm i}\,[E_i + {\rm Re}({\mit\Delta}_i)\,]\,t/\hbar)\, \exp[\,{\rm Im}({\mit\Delta}_i)\,t/\hbar] \,\vert i\rangle.$](img1979.png) |
(839) |
It is clear that the real part of
 gives rise to a simple
shift in energy of state
gives rise to a simple
shift in energy of state 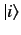 , whereas the imaginary part of
, whereas the imaginary part of
 governs the growth or decay of this state.
Thus,
governs the growth or decay of this state.
Thus,
![$\displaystyle \vert i, t\rangle = \exp[-{\rm i}\,(E_i + {\mit\Delta} E_i)\,t/\hbar] \exp( - {\mit\Gamma}_i\,t/2\,\hbar)\,\vert i\rangle,$](img1981.png) |
(840) |
where
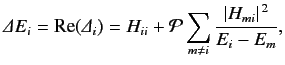 |
(841) |
and
 |
(842) |
Note that the energy-shift
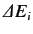 is the same as that predicted
by standard time-independent perturbation theory.
is the same as that predicted
by standard time-independent perturbation theory.
The probability of observing the system in state 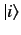 at time
at time 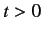 , given
that it is definately in state
, given
that it is definately in state 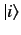 at time
at time 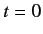 , is given by
, is given by
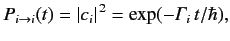 |
(843) |
where
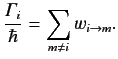 |
(844) |
Here, use has been made of Equation (817).
Clearly, the rate of decay of the initial state is a simple function of
the transition rates to the other states. Note that the system conserves
probability up to second order in perturbed quantities, because
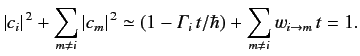 |
(845) |
The quantity
 is called the decay-width of state
is called the decay-width of state 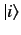 .
It is
closely related to the mean lifetime of this state,
.
It is
closely related to the mean lifetime of this state,
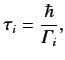 |
(846) |
where
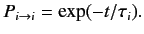 |
(847) |
According to Equation (839), the amplitude of state 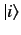 both oscillates
and decays as time progresses. Clearly, state
both oscillates
and decays as time progresses. Clearly, state 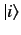 is not a
stationary state in the presence of the time-dependent perturbation.
However, we can still represent it as a superposition of stationary
states (whose amplitudes simply oscillate in time). Thus,
is not a
stationary state in the presence of the time-dependent perturbation.
However, we can still represent it as a superposition of stationary
states (whose amplitudes simply oscillate in time). Thus,
![$\displaystyle \exp[-{\rm i}\,(E_i + {\mit\Delta} E_i)\,t/\hbar] \exp( - {\mit\Gamma}_i\,t/2\,\hbar) = \int dE\,f(E) \exp(-{\rm i}\, E\,t/\hbar),$](img1991.png) |
(848) |
where  is the weight of the stationary state with energy
is the weight of the stationary state with energy 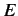 in the
superposition. The Fourier inversion theorem yields
in the
superposition. The Fourier inversion theorem yields
![$\displaystyle \vert f(E)\vert^{\,2} \propto \frac{1}{(E - [E_i +{\rm Re}({\mit\Delta}_i)])^2 + {\mit\Gamma}_i^{\,2}/4}.$](img1993.png) |
(849) |
In the absence of the perturbation,
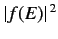 is basically a delta-function
centered on the unperturbed energy
is basically a delta-function
centered on the unperturbed energy 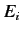 of state
of state 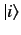 .
In other words, state
.
In other words, state 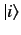 is a stationary state whose energy is
completely determined. In the presence of the perturbation, the energy
of state
is a stationary state whose energy is
completely determined. In the presence of the perturbation, the energy
of state 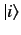 is shifted by
is shifted by
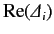 . The fact that
the state is no longer stationary (i.e., it decays in time) implies that
its energy cannot be exactly determined. Indeed, the
energy of the state
is smeared over some region of width (in energy)
. The fact that
the state is no longer stationary (i.e., it decays in time) implies that
its energy cannot be exactly determined. Indeed, the
energy of the state
is smeared over some region of width (in energy)
 centered
around the shifted energy
centered
around the shifted energy
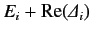 . The faster the
decay of the state (i.e., the larger
. The faster the
decay of the state (i.e., the larger
 ), the more its
energy is spread out. This effect is clearly a manifestation of
the energy-time uncertainty relation
), the more its
energy is spread out. This effect is clearly a manifestation of
the energy-time uncertainty relation
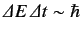 .
One consequence of this effect is the existence of a natural
width of spectral lines associated with the decay of some excited
state to the ground state (or any other lower energy state). The uncertainty
in energy of the excited state, due to its propensity to decay, gives
rise to a slight smearing (in wavelength)
of the spectral line associated with the
transition. Strong lines, which correspond to fast transitions, are smeared out
more that weak lines. For this reason, spectroscopists generally favor
forbidden lines (see Section 8.10) for Doppler-shift measurements. Such lines are not as bright
as those corresponding to allowed transitions, but they are a lot sharper.
.
One consequence of this effect is the existence of a natural
width of spectral lines associated with the decay of some excited
state to the ground state (or any other lower energy state). The uncertainty
in energy of the excited state, due to its propensity to decay, gives
rise to a slight smearing (in wavelength)
of the spectral line associated with the
transition. Strong lines, which correspond to fast transitions, are smeared out
more that weak lines. For this reason, spectroscopists generally favor
forbidden lines (see Section 8.10) for Doppler-shift measurements. Such lines are not as bright
as those corresponding to allowed transitions, but they are a lot sharper.



Next: Harmonic Perturbations
Up: Time-Dependent Perturbation Theory
Previous: Sudden Perturbations
Richard Fitzpatrick
2013-04-08
![]() . Thus,
. Thus,
![]() , the system is assumed to
be in the initial state
, the system is assumed to
be in the initial state ![]() . Thus,
. Thus,
![]() ,
and
,
and
![]() . Basically, we want to
calculate the time evolution of the coefficient
. Basically, we want to
calculate the time evolution of the coefficient ![]() .
First, however, let us check that our previous Fermi golden rule result
still applies when the perturbing potential is turned on slowly,
instead of very suddenly. For
.
First, however, let us check that our previous Fermi golden rule result
still applies when the perturbing potential is turned on slowly,
instead of very suddenly. For
![]() we have from Equations (795)-(796) that
we have from Equations (795)-(796) that
![$\displaystyle = - \frac{\rm i}{\hbar}\, H_{ni} \int_{-\infty}^t dt'\, \exp[(\et...
..., \frac{ \exp[(\eta + {\rm i}\,\omega_{ni} )\, t]}{\eta +{\rm i}\,\omega_{ni}},$](img1950.png)
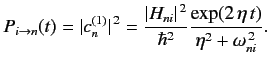
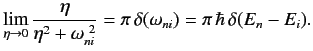
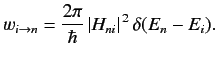
![]() using Equations (795)-(797). We have
using Equations (795)-(797). We have

![$\displaystyle = \left(\frac{-{\rm i}}{\hbar} \right)^2 \sum_m \vert H_{mi}\vert...
...xp[(\eta+ {\rm i}\,\omega_{im})\, t'] \exp[ (\eta+ {\rm i}\,\omega_{mi})\, t'']$](img1962.png)
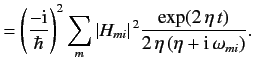
![]() , where
, where
![]() . Using Equation (831), we can evaluate this ratio in the limit
. Using Equation (831), we can evaluate this ratio in the limit
![]() . We obtain
. We obtain
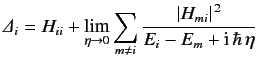
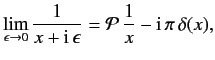

![]() . Thus, we obtain
. Thus, we obtain
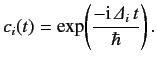
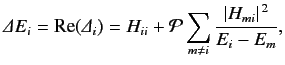

![]() at time
at time ![]() , given
that it is definately in state
, given
that it is definately in state ![]() at time
at time ![]() , is given by
, is given by
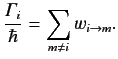
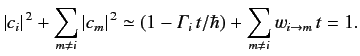
![]() is called the decay-width of state
is called the decay-width of state ![]() .
It is
closely related to the mean lifetime of this state,
.
It is
closely related to the mean lifetime of this state,
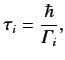
![$\displaystyle \exp[-{\rm i}\,(E_i + {\mit\Delta} E_i)\,t/\hbar] \exp( - {\mit\Gamma}_i\,t/2\,\hbar) = \int dE\,f(E) \exp(-{\rm i}\, E\,t/\hbar),$](img1991.png)
![$\displaystyle \vert f(E)\vert^{\,2} \propto \frac{1}{(E - [E_i +{\rm Re}({\mit\Delta}_i)])^2 + {\mit\Gamma}_i^{\,2}/4}.$](img1993.png)