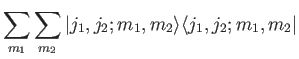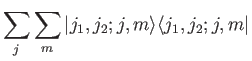Next: Clebsch-Gordon Coefficients
Up: Addition of Angular Momentum
Previous: Introduction
Consider the most general case. Suppose
that we have two sets of angular momentum operators, 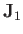 and
and 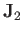 .
By definition, these operators are Hermitian, and obey the fundamental commutation
relations
.
By definition, these operators are Hermitian, and obey the fundamental commutation
relations
Let us assume that the two groups of operators correspond to different degrees
of freedom of the system, so that
![$\displaystyle [J_{1\,i}, J_{2\,j}] = 0,$](img1618.png) |
(6.3) |
where 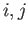 stand for either
stand for either  ,
, 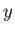 , or
, or 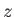 . (See Section 2.2.)
For instance,
. (See Section 2.2.)
For instance, 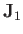 could be an orbital angular momentum operator, and
could be an orbital angular momentum operator, and 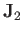 a spin angular momentum operator. Alternatively,
a spin angular momentum operator. Alternatively, 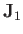 and
and 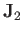 could
be the orbital angular momentum operators
of two different particles in a multi-particle
system. We know, from the general
properties of angular momentum outlined in the previous two chapters, that the eigenvalues of
could
be the orbital angular momentum operators
of two different particles in a multi-particle
system. We know, from the general
properties of angular momentum outlined in the previous two chapters, that the eigenvalues of 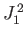 and
and 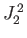 can be
written
can be
written
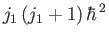 and
and
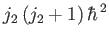 , respectively, where
, respectively, where
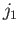 and
and 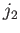 are either integers, or half-integers. We also know that the
eigenvalues of
are either integers, or half-integers. We also know that the
eigenvalues of 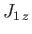 and
and 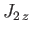 take the form
take the form
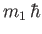 and
and
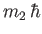 , respectively, where
, respectively, where 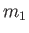 and
and 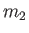 are numbers
lying in the ranges
are numbers
lying in the ranges
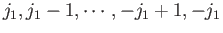 and
and
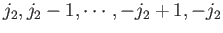 , respectively.
, respectively.
Let us define the total angular momentum operator
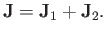 |
(6.4) |
Now, 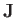 is an Hermitian operator, because it is the sum of Hermitian operators.
Moreover, according to Equation (4.14),
is an Hermitian operator, because it is the sum of Hermitian operators.
Moreover, according to Equation (4.14), 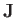 satisfies the fundamental commutation
relation
satisfies the fundamental commutation
relation
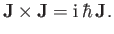 |
(6.5) |
Thus, 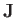 possesses all of the expected properties of an
angular momentum operator. It follows that the eigenvalue of
possesses all of the expected properties of an
angular momentum operator. It follows that the eigenvalue of 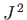 can be
written
can be
written
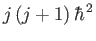 , where
, where 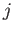 is an integer, or a half-integer. Moreover, the eigenvalue
of
is an integer, or a half-integer. Moreover, the eigenvalue
of 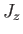 takes the form
takes the form 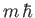 , where
, where 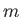 lies in the range
lies in the range
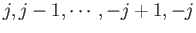 . At this stage, however, we do not know the relationship between the quantum
numbers of the total angular momentum,
. At this stage, however, we do not know the relationship between the quantum
numbers of the total angular momentum, 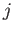 and
and 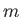 , and those of the
individual angular momenta,
, and those of the
individual angular momenta, 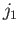 ,
, 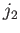 ,
, 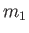 , and
, and 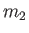 .
.
Now,
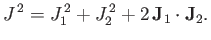 |
(6.6) |
Furthermore, we know that
and also that all of the 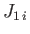 ,
, 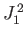 operators commute with the
operators commute with the 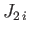 ,
, 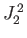 operators.
It follows from Equation (6.6) that
operators.
It follows from Equation (6.6) that
![$\displaystyle [J^{\,2}, J_1^{\,2}] = [J^{\,2}, J_2^{\,2}] = 0.$](img1645.png) |
(6.9) |
This implies that the quantum numbers 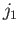 ,
, 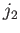 , and
, and 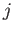 can all be measured
simultaneously. In other words, it is possible to determine the magnitude of the total
angular momentum together with the magnitudes of the component
angular momenta. However, it is apparent from Equations (6.1), (6.2), and (6.6)
that
can all be measured
simultaneously. In other words, it is possible to determine the magnitude of the total
angular momentum together with the magnitudes of the component
angular momenta. However, it is apparent from Equations (6.1), (6.2), and (6.6)
that
This suggests that it is not possible to measure the quantum numbers 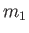 and
and 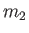 simultaneously with the quantum number
simultaneously with the quantum number 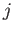 . Thus, we cannot determine
the projections of the individual angular momenta along the
. Thus, we cannot determine
the projections of the individual angular momenta along the 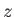 -axis together with the magnitude of the total angular momentum.
-axis together with the magnitude of the total angular momentum.
It is clear, from the preceding discussion, that we can form two alternate groups
of mutually commuting operators. The first group
is
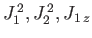 , and
, and
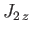 . The second group is
. The second group is
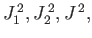 and
and 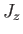 . These two
groups of operators are incompatible with one another. We can define simultaneous
eigenkets of each operator group. The simultaneous eigenkets of
. These two
groups of operators are incompatible with one another. We can define simultaneous
eigenkets of each operator group. The simultaneous eigenkets of
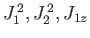 , and
, and
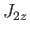 are denoted
are denoted
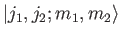 , where
, where
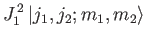 |
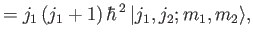 |
(6.12) |
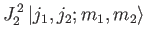 |
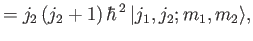 |
(6.13) |
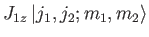 |
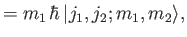 |
(6.14) |
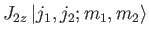 |
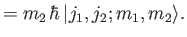 |
(6.15) |
The simultaneous eigenkets of
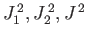 and
and 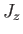 are denoted
are denoted
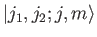 , where
, where
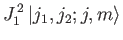 |
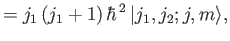 |
(6.16) |
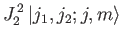 |
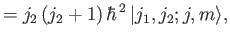 |
(6.17) |
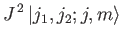 |
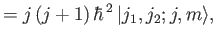 |
(6.18) |
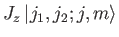 |
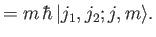 |
(6.19) |
Each set of eigenkets are complete, mutually orthogonal (for eigenkets corresponding
to different sets of eigenvalues), and have unit norms. Because the operators
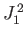 and
and 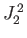 are common to both operator groups, we can assume
that the quantum numbers
are common to both operator groups, we can assume
that the quantum numbers 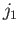 and
and 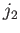 are known. In other words, we
can always determine
the magnitudes of the individual angular momenta. In addition, we can either
know the quantum numbers
are known. In other words, we
can always determine
the magnitudes of the individual angular momenta. In addition, we can either
know the quantum numbers 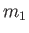 and
and 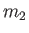 , or the quantum numbers
, or the quantum numbers 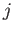 and
and
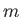 , but we cannot know both pairs of quantum numbers at the same time.
Finally, we can write a conventional completeness relation for both sets of
eigenkets:
, but we cannot know both pairs of quantum numbers at the same time.
Finally, we can write a conventional completeness relation for both sets of
eigenkets:
where the right-hand sides denote the identity operator in the ket space corresponding
to states of given 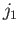 and
and 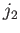 . The summation is over all allowed values
of
. The summation is over all allowed values
of 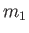 ,
, 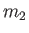 ,
, 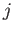 , and
, and 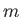 .
.



Next: Clebsch-Gordon Coefficients
Up: Addition of Angular Momentum
Previous: Introduction
Richard Fitzpatrick
2016-01-22
![]() , and
, and
![]() . The second group is
. The second group is
![]() and
and ![]() . These two
groups of operators are incompatible with one another. We can define simultaneous
eigenkets of each operator group. The simultaneous eigenkets of
. These two
groups of operators are incompatible with one another. We can define simultaneous
eigenkets of each operator group. The simultaneous eigenkets of
![]() , and
, and
![]() are denoted
are denoted
![]() , where
, where