

Next: Addition of Angular Momentum
Up: Spin Angular Momentum
Previous: Spin Greater Than One-Half
- Demonstrate that the operators defined in Equations (5.11)-(5.13) are Hermitian, and
satisfy
the commutation relations (5.1).
- Prove the Baker-Campbell-Hausdorff lemma, (5.31).
- Let the
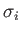 , for
, for 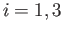 , be the three spin-
, be the three spin-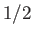 Pauli matrices. Demonstrate that
Pauli matrices. Demonstrate that
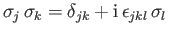 , and, hence, that
, and, hence, that
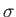
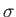
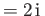
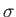 and
and
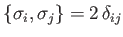 .
.
- Find the Pauli representations of the normalized eigenstates of (a)
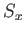 and (b)
and (b) 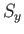 for
a spin-
for
a spin-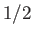 particle.
particle.
- Suppose that a spin-
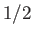 particle
has a spin vector that lies in the
particle
has a spin vector that lies in the 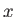 -
-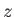 plane, making an
angle
plane, making an
angle 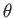 with the
with the 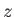 -axis. Demonstrate that a measurement of
-axis. Demonstrate that a measurement of 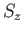 yields
yields 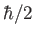 with probability
with probability
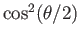 , and
, and 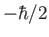 with probability
with probability
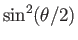 .
.
- An electron is in the spin-state
in the Pauli representation. (a) Determine the constant 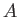 by normalizing
by normalizing
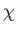 . (b) If a measurement of
. (b) If a measurement of 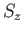 is made, what values will be
obtained, and with what probabilities? What is the expectation
value of
is made, what values will be
obtained, and with what probabilities? What is the expectation
value of 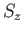 ? Repeat the previous calculations for (c)
? Repeat the previous calculations for (c) 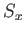 and (d)
and (d) 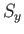 . [61]
. [61]
- Consider a spin-
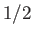 system represented by the normalized spinor
system represented by the normalized spinor
in the Pauli representation, where 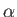 and
and 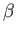 are real. What is the probability that a measurement of
are real. What is the probability that a measurement of
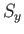 yields
yields 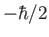 ? [53]
? [53]
- An electron is at rest in an oscillating magnetic field
where 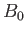 and
and 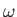 are real positive constants.
are real positive constants.
- Find the Hamiltonian of the system.
- If the electron starts in the spin-up state with respect to the
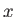 -axis, determine the spinor
-axis, determine the spinor 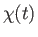 that represents the state
of the system in the Pauli representation at all subsequent times.
that represents the state
of the system in the Pauli representation at all subsequent times.
- Find the probability that a measurement of
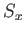 yields
the result
yields
the result 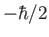 as a function of time.
as a function of time.
- What is the minimum value of
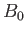 required to force a
complete flip in
required to force a
complete flip in 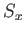 ?
?
- In the Schrödinger/Pauli representation, the generalization of Schrödinger's time-dependent
wave equation for an electron moving in electromagnetic fields is written
where 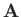 the
vector potential,
the
vector potential,
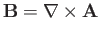 the magnetic field-strength,
the magnetic field-strength, 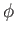 the scalar potential, and
the scalar potential, and 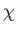 the spinor-wavefunction. The term involving the
Pauli matrices comes from the electron's intrinsic magnetic moment. (See Section 5.5.)
Demonstrate that this equation can also be written
the spinor-wavefunction. The term involving the
Pauli matrices comes from the electron's intrinsic magnetic moment. (See Section 5.5.)
Demonstrate that this equation can also be written
The previous expression is known as the Pauli equation [80].
- Let
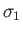 ,
, 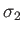 , and
, and 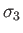 be the Pauli matrices for a spin-
be the Pauli matrices for a spin-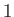 particle.
particle.
- Show that
where
- Show that
where
- Show that
where
- Hence, deduce that the spinor matrices for rotations through an
angle
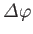 about the three Cartesian axes are
about the three Cartesian axes are
where
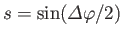 and
and
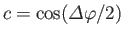 .
.
- Suppose that a spin-
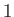 particle
has a spin vector that lies in the
particle
has a spin vector that lies in the 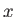 -
-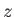 plane, making an
angle
plane, making an
angle 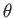 with the
with the 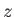 -axis. Demonstrate that a measurement of
-axis. Demonstrate that a measurement of 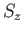 yields
yields 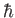 , 0
, and
, 0
, and 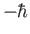 with probabilities
with probabilities
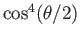 ,
,
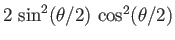 ,
and
,
and
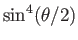 , respectively.
, respectively.


Next: Addition of Angular Momentum
Up: Spin Angular Momentum
Previous: Spin Greater Than One-Half
Richard Fitzpatrick
2016-01-22
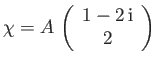
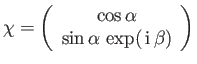
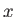 -axis, determine the spinor
-axis, determine the spinor 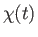 that represents the state
of the system in the Pauli representation at all subsequent times.
that represents the state
of the system in the Pauli representation at all subsequent times.
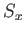 yields
the result
yields
the result 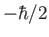 as a function of time.
as a function of time.
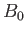 required to force a
complete flip in
required to force a
complete flip in 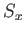 ?
?
![$\displaystyle {\rm i}\,\hbar\,\frac{\partial\chi}{\partial t} = \frac{1}{2\,m_e...
...A})+e\,\hbar\,\mbox{\boldmath $\sigma$}\cdot{\bf B}\right]\chi -e\,\phi\,\chi,
$](img1583.png)
![$\displaystyle {\rm i}\,\hbar\,\frac{\partial\chi}{\partial t} = \frac{1}{2\,m_e...
...$\sigma$}\cdot (-{\rm i}\,\hbar\,\nabla+e\,{\bf A})\right]\chi -e\,\phi\,\chi.
$](img1585.png)
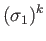
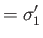
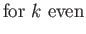
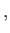
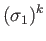
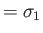
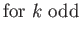
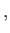
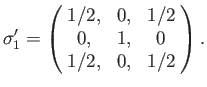
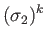
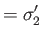
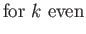
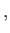
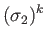
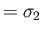
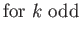
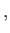
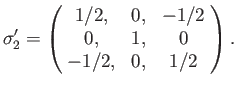
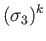
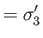
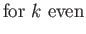
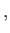
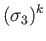

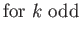
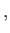
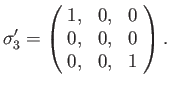
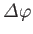 about the three Cartesian axes are
about the three Cartesian axes are
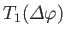
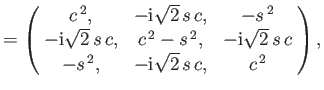
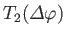
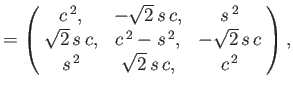
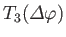
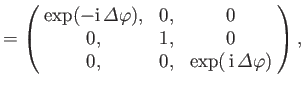
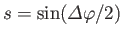 and
and
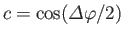 .
.
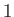 particle
has a spin vector that lies in the
particle
has a spin vector that lies in the 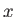 -
-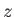 plane, making an
angle
plane, making an
angle 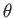 with the
with the 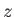 -axis. Demonstrate that a measurement of
-axis. Demonstrate that a measurement of 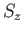 yields
yields 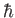 , 0
, and
, 0
, and 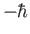 with probabilities
with probabilities
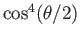 ,
,
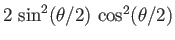 ,
and
,
and
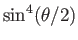 , respectively.
, respectively.