Next: Perturbed Magnetic Field Up: Toroidal Tearing Modes Previous: Equilibrium Plasma Current Density Contents
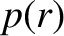 be the equilibrium plasma pressure profile.
The equilibrium force balance relation (see Section 2.25)
be the equilibrium plasma pressure profile.
The equilibrium force balance relation (see Section 2.25)
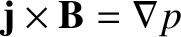 |
(14.30) |
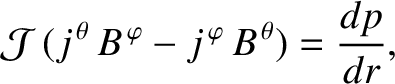 |
(14.31) |
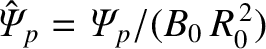 ,
,
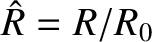 ,
,
 , and
, and
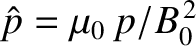 .
.