Next: Langmuir Sheaths Up: Plasma Fluid Theory Previous: Drift Equations Contents
 ).
).
In the limit
 , the cold-plasma equations reduce to
, the cold-plasma equations reduce to
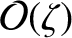 .
Note that none of the remaining terms in these equations depend
explicitly on collisions. Nevertheless, the absence of collisions
poses a serious problem. Whereas the magnetic field effectively confines
charged particles in directions perpendicular to magnetic field-lines,
by forcing them to execute tight Larmor orbits, we have now lost all
confinement along field-lines. But, does this matter?
.
Note that none of the remaining terms in these equations depend
explicitly on collisions. Nevertheless, the absence of collisions
poses a serious problem. Whereas the magnetic field effectively confines
charged particles in directions perpendicular to magnetic field-lines,
by forcing them to execute tight Larmor orbits, we have now lost all
confinement along field-lines. But, does this matter?
The typical frequency associated with fluid motion
is the transit frequency, 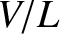 . However, according to Equation (4.154),
the cold-plasma ordering implies that the transit frequency is of similar magnitude to a
typical gyrofrequency:
. However, according to Equation (4.154),
the cold-plasma ordering implies that the transit frequency is of similar magnitude to a
typical gyrofrequency:
 |
(4.229) |
Let us now consider the MHD limit. In this case, the typical transit frequency is
Thus, charged particles typically drift a distance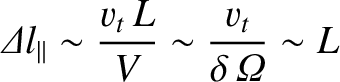 |
(4.231) |
In fact, in collisionless plasmas, MHD theory is replaced by a theory known as kinetic-MHD (Kruskal and Oberman 1958; Rosenbluth and Rostoker 1959). The latter theory is a combination of a one-dimensional kinetic theory, describing particle motion along magnetic field-lines, and a two-dimensional fluid theory, describing perpendicular motion. Unfortunately, the equations of kinetic-MHD are considerably more complicated that the conventional MHD equations. Is there any situation in which we can salvage the simpler MHD equations in a collisionless plasma? Fortunately, there is one case in which this is possible.
It turns out that in both varieties of MHD the motion of the plasma parallel to magnetic field-lines is associated with the dynamics of sound waves, whereas the motion perpendicular to field-lines is associated with the dynamics of a new type of wave called an Alfvén wave. As we shall see, in Chapter 5, Alfvén waves involve the “twanging” motion of magnetic field-lines—a little like the twanging of guitar strings. It is only the sound wave dynamics that are significantly modified when we move from a collisional to a collisionless plasma. It follows, therefore, that the MHD equations remain a reasonable approximation in a collisionless plasma in situations where the dynamics of sound waves, parallel to the magnetic field, are unimportant compared to the dynamics of Alfvén waves, perpendicular to the field. This situation arises whenever the parameter
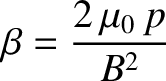 |
(4.232) |
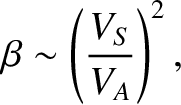 |
(4.233) |
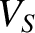 is the sound speed (i.e., thermal velocity), and
is the sound speed (i.e., thermal velocity), and 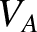 is the speed of an Alfvén wave. Thus, the inequality
is the speed of an Alfvén wave. Thus, the inequality
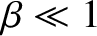 |
(4.234) |
We conclude, therefore, that in a low-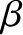 , collisionless, magnetized
plasma, the MHD equations,
, collisionless, magnetized
plasma, the MHD equations,
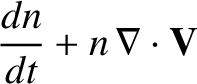 |
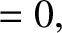 |
(4.235) |
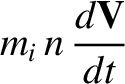 |
 |
(4.236) |
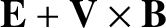 |
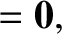 |
(4.237) |
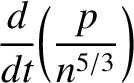 |
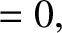 |
(4.238) |
Let us, finally, consider the drift limit. In this case, the typical transit frequency is
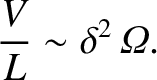 |
(4.239) |
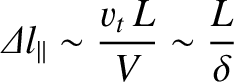 |
(4.240) |
Now, in the drift limit, the perpendicular drift velocity of
charged particles, which is a combination of
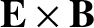 drift,
grad-
drift,
grad-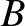 drift, and curvature drift (see Chapter 2), is approximately
drift, and curvature drift (see Chapter 2), is approximately
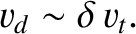 |
(4.241) |
 |
(4.242) |
In fact, in collisionless plasmas, Braginskii-type transport theory—conventionally known as classical transport theory—is replaced by a new theory—known as neoclassical transport theory—which is a combination of a two-dimensional kinetic theory, describing particle motion on drift surfaces, and a one-dimensional fluid theory, describing motion perpendicular to the drift surfaces (Bernstein 1974; Hinton and Hazeltine 1976). Here, a drift surface is a closed surface formed by the locus of a charged particle's drift orbit (including drifts parallel and perpendicular to the magnetic field). Of course, the orbits only form closed surfaces if the plasma is confined, but there is little point in examining transport in an unconfined plasma. Unlike classical transport theory, which is strictly local in nature, neoclassical transport theory is nonlocal, in the sense that the transport coefficients depend on the average values of plasma properties taken over drift surfaces.