Next: Low-Frequency Wave Propagation Up: Waves in Cold Plasmas Previous: Cutoff and Resonance Contents
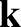 is directed along the
is directed along the  -axis (i.e.,
-axis (i.e., 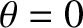 ).
In the zero magnetic field limit (i.e.,
).
In the zero magnetic field limit (i.e.,
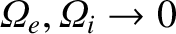 ), the eigenmode equation (5.42) reduces to
where
), the eigenmode equation (5.42) reduces to
where
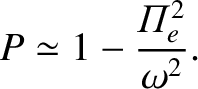 |
(5.69) |
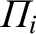 with respect to
with respect to
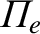 .
.
It is clear from Equation (5.68) that there are two types of waves.
The first possesses
the eigenvector
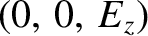 , and has the dispersion relation
, and has the dispersion relation
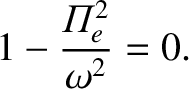 |
(5.70) |
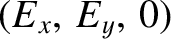 , and has the dispersion
relation
Here,
, and has the dispersion
relation
Here, 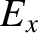 ,
, 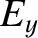 , and
, and 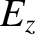 are arbitrary non-zero quantities.
are arbitrary non-zero quantities.
The former wave has 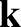 parallel to
parallel to 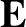 , and is, thus, a
longitudinal (with respect to the electric field) wave. This wave is known as the plasma wave, and
possesses the fixed frequency
, and is, thus, a
longitudinal (with respect to the electric field) wave. This wave is known as the plasma wave, and
possesses the fixed frequency
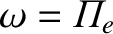 . Now, if
. Now, if
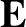 is parallel to
is parallel to 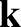 then it follows from Equation (5.5)
that
then it follows from Equation (5.5)
that
 . In other words, the plasma wave is purely electrostatic
in nature. In fact, the plasma wave is an electrostatic oscillation of the type
discussed in Section 1.4.
Because
. In other words, the plasma wave is purely electrostatic
in nature. In fact, the plasma wave is an electrostatic oscillation of the type
discussed in Section 1.4.
Because 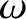 is independent of
is independent of 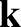 , the so-called group-velocity (Fitzpatrick 2013),
, the so-called group-velocity (Fitzpatrick 2013),
The latter wave is a transverse wave, with 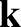 perpendicular to
perpendicular to
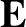 . There are two independent linear polarizations of this wave,
which propagate at identical velocities,
just like a vacuum electromagnetic wave. The dispersion relation
(5.71) can be rearranged to give
. There are two independent linear polarizations of this wave,
which propagate at identical velocities,
just like a vacuum electromagnetic wave. The dispersion relation
(5.71) can be rearranged to give
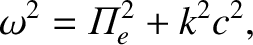 |
(5.73) |
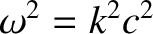 , modified by
the presence of the plasma. An important conclusion, which follows
immediately from the previous expression, is that this wave can only propagate if
, modified by
the presence of the plasma. An important conclusion, which follows
immediately from the previous expression, is that this wave can only propagate if
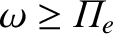 . Because
. Because
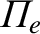 is
proportional to the square root of the electron number density, it follows that
electromagnetic radiation of a given frequency can only propagate through
an unmagnetized plasma when the electron number density falls below some critical value.
is
proportional to the square root of the electron number density, it follows that
electromagnetic radiation of a given frequency can only propagate through
an unmagnetized plasma when the electron number density falls below some critical value.