Next: Braginskii Equations Up: Plasma Fluid Theory Previous: Fluid Closure Contents
Consider a neutral gas consisting of identical hard-sphere molecules of
mass 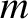 and
diameter
and
diameter 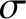 . Admittedly, this is not a particularly
physical model of a neutral gas,
but we are only considering it for illustrative purposes. The fluid
equations for such a gas are similar to Equations (4.47)–(4.49):
. Admittedly, this is not a particularly
physical model of a neutral gas,
but we are only considering it for illustrative purposes. The fluid
equations for such a gas are similar to Equations (4.47)–(4.49):
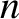 is the particle number density,
is the particle number density, 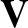 the flow velocity,
the flow velocity,
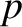 the scalar pressure,
and
the scalar pressure,
and 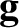 the acceleration due to gravity.
We have dropped the subscript
the acceleration due to gravity.
We have dropped the subscript  because, in this case, there is
only a single species. There is no collisional friction or heating
in a single species system.
Of course, there are no electrical or magnetic forces in
a neutral gas, so we have included gravitational forces instead.
The purpose of the closure scheme is to express the
viscosity tensor,
because, in this case, there is
only a single species. There is no collisional friction or heating
in a single species system.
Of course, there are no electrical or magnetic forces in
a neutral gas, so we have included gravitational forces instead.
The purpose of the closure scheme is to express the
viscosity tensor,
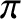 , and the heat flux density,
, and the heat flux density, 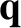 , in terms
of
, in terms
of 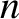 ,
, 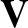 , or
, or 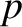 , and, thereby, complete the set of equations.
, and, thereby, complete the set of equations.
The mean-free-path, 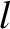 , for hard-sphere molecules is given by
, for hard-sphere molecules is given by
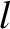 is completely independent of the speed or
mass of the molecules. The mean-free-path is assumed to be much
smaller than the variation lengthscale,
is completely independent of the speed or
mass of the molecules. The mean-free-path is assumed to be much
smaller than the variation lengthscale, 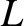 , of macroscopic quantities,
so that
, of macroscopic quantities,
so that
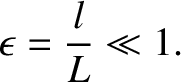 |
(4.59) |
In the Chapman-Enskog scheme, the distribution function is expanded, order by order,
in the small parameter 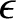 :
:
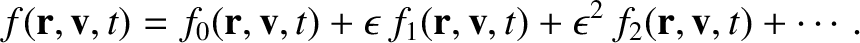 |
(4.60) |
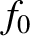 ,
, 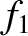 ,
, 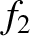 , and so on, are all assumed to be of the same order of
magnitude. In fact, only the first two terms in this expansion are ever
calculated.
To zeroth order in
, and so on, are all assumed to be of the same order of
magnitude. In fact, only the first two terms in this expansion are ever
calculated.
To zeroth order in 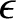 , the kinetic equation requires that
, the kinetic equation requires that 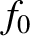 be
a Maxwellian:
be
a Maxwellian:
![$\displaystyle f_0({\bf r}, {\bf v}, t) = n({\bf r})
\left[\frac{m}{2\pi\,T({\bf...
...ght]^{3/2}\,\exp\!\left[-\frac{m\,({\bf v}-
{\bf V})^2}
{2\,T({\bf r})}\right].$](img1112.png) |
(4.61) |
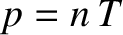 . As is well known, there is zero heat flow or viscous stress associated
with a Maxwellian distribution function (Reif 1965). Thus, both the heat flux density,
. As is well known, there is zero heat flow or viscous stress associated
with a Maxwellian distribution function (Reif 1965). Thus, both the heat flux density,
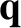 ,
and the viscosity tensor,
,
and the viscosity tensor,
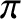 , depend on the first-order
non-Maxwellian correction
to the distribution function,
, depend on the first-order
non-Maxwellian correction
to the distribution function, 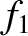 .
.
It is possible to linearize the kinetic equation, and then rearrange
it so as to obtain an integral equation for 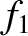 in terms of
in terms of 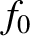 .
This rearrangement crucially depends on the bilinearity of the collision
operator.
Incidentally, the equation is integral because the collision operator is an integral
operator. The integral equation is solved by expanding
.
This rearrangement crucially depends on the bilinearity of the collision
operator.
Incidentally, the equation is integral because the collision operator is an integral
operator. The integral equation is solved by expanding 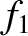 in velocity space
using Laguerre polynomials (sometimes called Sonine polynomials) (Abramowitz and Stegun 1965). It is
possible to reduce the integral equation to an infinite set of simultaneous
algebraic equations for the coefficients in this expansion. If the expansion
is truncated, after
in velocity space
using Laguerre polynomials (sometimes called Sonine polynomials) (Abramowitz and Stegun 1965). It is
possible to reduce the integral equation to an infinite set of simultaneous
algebraic equations for the coefficients in this expansion. If the expansion
is truncated, after 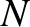 terms, say, then these algebraic equations can be solved for
the coefficients. It turns out that the Laguerre polynomial expansion
converges very rapidly. Thus, it is conventional to keep only the first two
terms in this expansion, which is usually sufficient to ensure an accuracy of
about
terms, say, then these algebraic equations can be solved for
the coefficients. It turns out that the Laguerre polynomial expansion
converges very rapidly. Thus, it is conventional to keep only the first two
terms in this expansion, which is usually sufficient to ensure an accuracy of
about 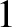 percent in the final result. Finally, the appropriate moments
of
percent in the final result. Finally, the appropriate moments
of 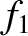 are taken, so as to obtain expression for the heat flux density
and the viscosity
tensor. Strictly speaking, after evaluating
are taken, so as to obtain expression for the heat flux density
and the viscosity
tensor. Strictly speaking, after evaluating 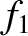 , we should then go on to
evaluate
, we should then go on to
evaluate 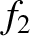 , so as to ensure that
, so as to ensure that 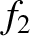 really is negligible compared to
really is negligible compared to 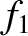 .
In reality, this is never done because the mathematical difficulties involved
in such a calculation are prohibitive.
.
In reality, this is never done because the mathematical difficulties involved
in such a calculation are prohibitive.
The Chapman-Enskog method outlined previously can be applied to any assumed force law between molecules, provided that the force is sufficiently short-range (i.e., provided that it falls off faster with increasing separation than the Coulomb force). For all sensible force laws, the viscosity tensor is given by
whereas the heat flux density takes the form Here,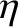 is the coefficient of viscosity, and
is the coefficient of viscosity, and 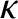 is the
coefficient of thermal conductivity. It is convenient to write
is the
coefficient of thermal conductivity. It is convenient to write
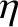 |
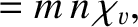 |
(4.64) |
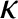 |
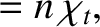 |
(4.65) |
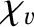 is the viscous diffusivity and
is the viscous diffusivity and
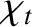 is the thermal diffusivity. Both
is the thermal diffusivity. Both
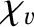 and
and
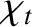 have the dimensions of length squared over time, and are,
effectively, diffusion coefficients. For the special
case of hard-sphere molecules, Chapman-Enskog theory yields (Chapman and Cowling 1953):
Here,
is the collision frequency,
and
have the dimensions of length squared over time, and are,
effectively, diffusion coefficients. For the special
case of hard-sphere molecules, Chapman-Enskog theory yields (Chapman and Cowling 1953):
Here,
is the collision frequency,
and
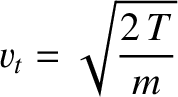 |
(4.69) |
Equations (4.66) and (4.67) have a simple physical interpretation. The viscous and thermal
diffusivities of a neutral gas can be accounted for in terms of the
random-walk diffusion of molecules with excess momentum and energy, respectively.
Recall the standard result in stochastic theory that if particles
jump an average distance 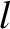 , in a random direction,
, in a random direction, 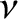 times a second, then
the diffusivity associated with such motion is
times a second, then
the diffusivity associated with such motion is
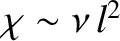 (Reif 1965).
Chapman-Enskog theory basically allows us to calculate the numerical constants
(Reif 1965).
Chapman-Enskog theory basically allows us to calculate the numerical constants
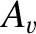 and
and 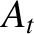 ,
multiplying
,
multiplying
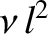 in the expressions for
in the expressions for 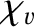 and
and 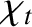 ,
for a given force law between molecules.
Obviously, these coefficients are different for different force laws. The
expression for the
mean-free-path,
,
for a given force law between molecules.
Obviously, these coefficients are different for different force laws. The
expression for the
mean-free-path, 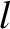 , is also different for different force laws.
, is also different for different force laws.