Next: Chapman-Enskog Closure Up: Plasma Fluid Theory Previous: Entropy Production Contents
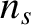 , the
flow velocity,
, the
flow velocity, 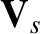 , and the scalar pressure,
, and the scalar pressure, 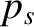 , to unknown quantities,
such as the viscosity tensor,
, to unknown quantities,
such as the viscosity tensor,
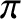
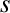 , the heat flux
density,
, the heat flux
density, 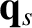 , and the
moments of the collision operator,
, and the
moments of the collision operator, 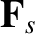 and
and 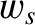 . In order to complete
our set of equations, we need to use some additional information to express the
latter quantities in terms of the former. This process is known as closure.
. In order to complete
our set of equations, we need to use some additional information to express the
latter quantities in terms of the former. This process is known as closure.
Lack of closure is an endemic problem in fluid theory. Because each moment is coupled to the next higher moment (for instance, the density evolution depends on the flow velocity, the flow velocity evolution depends on the viscosity tensor, and so on), any finite set of exact moment equations is bound to contain more unknowns than equations.
There are two basic types of fluid closure schemes. In truncation schemes, higher order moments of the distribution function are assumed to vanish, or are prescribed in terms of lower moments (Grad 1958). Truncation schemes are relatively straightforward to implement, but the error associated with the closure cannot easily be determined. Asymptotic schemes, on the other hand, depend on the rigorous exploitation of some small parameter. Asymptotic closure schemes have the advantage of providing some estimate of the error involved in the closure. On the other hand, the asymptotic approach to closure is mathematically demanding, because it inevitably involves working with the kinetic equation.