One mechanism for obtaining fast magnetic reconnection (i.e., faster than Sweet-Parker reconnection) is via
the plasmoid instability (Loureiro, et al. 2007; Bhattacharjee, et al. 2009). This instability causes
Sweet-Parker current sheets to break up into chains of secondary magnetic islands (plasmoids).
Consider the linear stability of a current sheet of the form (9.17), whose thickness in the 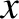 -direction is
-direction is  . It is helpful to define the
Alfvén time,
. It is helpful to define the
Alfvén time,
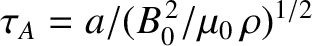 , as well as the modified Lundquist number,
, as well as the modified Lundquist number,
 . Note that
. Note that 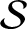 has no dependence on the wavelength,
has no dependence on the wavelength,  , of the instability in the
, of the instability in the 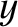 -direction. Let
us assume that
-direction. Let
us assume that 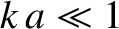 . It follows from Equation (9.39) that
. It follows from Equation (9.39) that
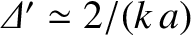 . According to the analysis of Section 9.5, if the instability is in the constant-
. According to the analysis of Section 9.5, if the instability is in the constant- regime then
regime then
where 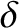 is the linear layer thickness (Bhattacharjee, et al. 2009). The previous two equations are valid provided that
is the linear layer thickness (Bhattacharjee, et al. 2009). The previous two equations are valid provided that
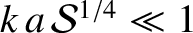 . On the other hand, according to the analysis of Section 9.6, if the instability is in the non-constant-
. On the other hand, according to the analysis of Section 9.6, if the instability is in the non-constant- regime then
The previous two equations are valid provided that
regime then
The previous two equations are valid provided that
 . Equations (9.155)–(9.158) suggest that the growth-rate of the instability attains a
maximum value,
. Equations (9.155)–(9.158) suggest that the growth-rate of the instability attains a
maximum value,
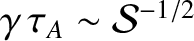 , when
, when
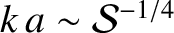 and
and
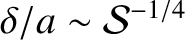 .
Note that the maximum growth-rate occurs at the boundary between the constant-
.
Note that the maximum growth-rate occurs at the boundary between the constant- and non-constant-
and non-constant- regimes.
regimes.
Figure: 9.11
Dispersion relation for the plasmoid instability. The horizontal and vertical dotted lines
correspond to
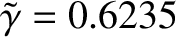 and
and
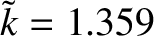 , respectively.
, respectively.
|
|
We can determine the maximum growth-rate exactly making use of the general linear dispersion relation (9.81).
Let
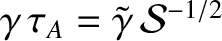 and
and
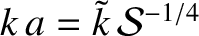 . For the case in
hand, the dispersion relation yields
. For the case in
hand, the dispersion relation yields
![$\displaystyle \tilde{k} = \left[-\frac{16}{\pi}\,Q^{-5/4}\,\frac{\Gamma(Q^{3/2}/4+5/4)}{\Gamma(Q^{3/2}/4-1/4)}\right]^{3/4},$](img3695.png) |
(9.159) |
where
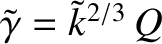 . Figure 9.11 shows the variation of
. Figure 9.11 shows the variation of
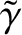 with
with
 obtained from the previous equation. It can be seen that
obtained from the previous equation. It can be seen that
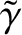 attains a
maximum value of
attains a
maximum value of 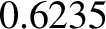 when
when
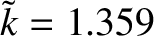 .
Thus, if
.
Thus, if 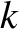 is unconstrained then the fastest growing instability of a
current sheet is such that
is unconstrained then the fastest growing instability of a
current sheet is such that
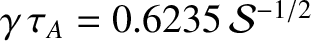 and
and
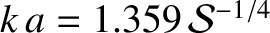 .
.
Let us now apply the previous analysis to a Sweet-Parker current sheet. According to Equations (9.84), (9.146), and (9.150), the thickness of a Sweet-Parker current sheet is
 |
(9.160) |
where
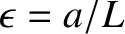 , and
, and 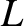 is the periodicity length of the primary magnetic island chain in the
is the periodicity length of the primary magnetic island chain in the 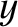 -direction. (Thus, the wavenumber of the island chain is
-direction. (Thus, the wavenumber of the island chain is  .)
Let
us assume that
.)
Let
us assume that
 , as is generally the case in non-constant-
, as is generally the case in non-constant- island chains. Given that
island chains. Given that
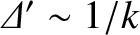 , it follows that
, it follows that
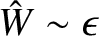 . Hence,
. Hence,
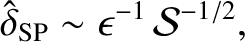 |
(9.161) |
where
 . We can use the previous analysis to find the fastest growing
instability of the Sweet-Parker current sheet by making the substitutions
. We can use the previous analysis to find the fastest growing
instability of the Sweet-Parker current sheet by making the substitutions
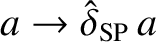 ,
,
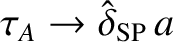 , and
, and
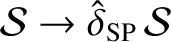 .
Thus, the fastest growing instability has a growth-rate
.
Thus, the fastest growing instability has a growth-rate
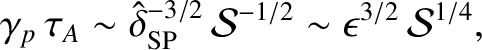 |
(9.162) |
and a wavenumber
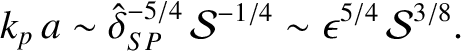 |
(9.163) |
It follows that the Sweet-Parker current sheet breaks up into a chain of secondary magnetic islands, or plasmoids,
whose wavelength is 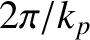 . Thus, the number of plasmoids in the island chain is
. Thus, the number of plasmoids in the island chain is
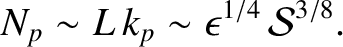 |
(9.164) |
The plasmoids are accelerated along the length of the current sheet and eventually expelled from its
two ends at the Alfvén velocity. Recall, from Equation (9.154), that the linear growth-rate of the primary instability matches the nonlinear growth-rate at the boundary between the linear and nonlinear regimes. It is, therefore,
reasonable to assume that the linear growth-rate of the secondary instability is similar in magnitude to its
initial nonlinear growth-rate. This suggests that the plasmoid instability is able to reconnect magnetic flux at
a much faster rate that the Sweet-Parker mechanism. In fact, the timescale for the plasmoid instablity to
achieve full reconnection is estimated as
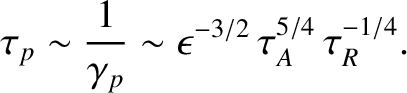 |
(9.165) |
This is a significantly shorter timescale that that associated with Sweet-Parker reconnection,
 |
(9.166) |
especially in a high Lundquist number plasma in which
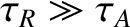 . Note that the normalized thickness of the
secondary Sweet-Parker current sheets that connect the plasmoids is
. Note that the normalized thickness of the
secondary Sweet-Parker current sheets that connect the plasmoids is
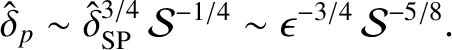 |
(9.167) |
The previous analysis gives the impression that all Sweet-Parker current sheets are unstable to the plasmoid
instability. In fact, this is not the case. In order for the analysis to remain valid there needs to be a reasonable
separation between the thickness of the primary Sweet-Parker current sheet,
 , and that of
the secondary Sweet-Parker current sheets,
, and that of
the secondary Sweet-Parker current sheets,  . Say,
. Say,
 |
(9.168) |
(Loureiro, et al. 2007). The previous relation leads to the plasmoid instablity criterion
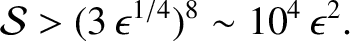 |
(9.169) |
In other words, the plasmoid instability only occurs when the Lundquist number exceeds a critical
value that is of order 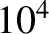 (assuming that
(assuming that
 ). This instability criterion has been verified numerically (Bhattacharjee, et al. 2009).
). This instability criterion has been verified numerically (Bhattacharjee, et al. 2009).
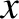 -direction is
-direction is  . It is helpful to define the
Alfvén time,
. It is helpful to define the
Alfvén time,
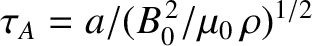 , as well as the modified Lundquist number,
, as well as the modified Lundquist number,
 . Note that
. Note that 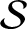 has no dependence on the wavelength,
has no dependence on the wavelength,  , of the instability in the
, of the instability in the 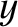 -direction. Let
us assume that
-direction. Let
us assume that 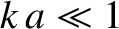 . It follows from Equation (9.39) that
. It follows from Equation (9.39) that
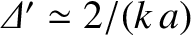 . According to the analysis of Section 9.5, if the instability is in the constant-
. According to the analysis of Section 9.5, if the instability is in the constant- regime then
regime then
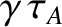
![$\displaystyle = \left[\frac{\Gamma(1/4)}{\pi\,\Gamma(3/4)}\right]^{4/5}(k\,a)^{-2/5}\,{\cal S}^{-3/5},$](img3680.png)


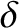 is the linear layer thickness (Bhattacharjee, et al. 2009). The previous two equations are valid provided that
is the linear layer thickness (Bhattacharjee, et al. 2009). The previous two equations are valid provided that
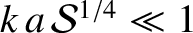 . On the other hand, according to the analysis of Section 9.6, if the instability is in the non-constant-
. On the other hand, according to the analysis of Section 9.6, if the instability is in the non-constant- regime then
regime then
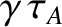
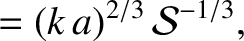

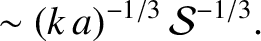
 . Equations (9.155)–(9.158) suggest that the growth-rate of the instability attains a
maximum value,
. Equations (9.155)–(9.158) suggest that the growth-rate of the instability attains a
maximum value,
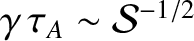 , when
, when
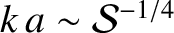 and
and
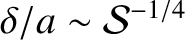 .
Note that the maximum growth-rate occurs at the boundary between the constant-
.
Note that the maximum growth-rate occurs at the boundary between the constant- and non-constant-
and non-constant- regimes.
regimes.
![\includegraphics[height=3.5in]{Chapter09/fig9_11.eps}](img3690.png)
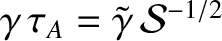 and
and
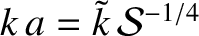 . For the case in
hand, the dispersion relation yields
. For the case in
hand, the dispersion relation yields
![$\displaystyle \tilde{k} = \left[-\frac{16}{\pi}\,Q^{-5/4}\,\frac{\Gamma(Q^{3/2}/4+5/4)}{\Gamma(Q^{3/2}/4-1/4)}\right]^{3/4},$](img3695.png)
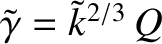 . Figure 9.11 shows the variation of
. Figure 9.11 shows the variation of
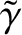 with
with
 obtained from the previous equation. It can be seen that
obtained from the previous equation. It can be seen that
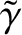 attains a
maximum value of
attains a
maximum value of 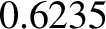 when
when
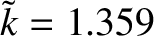 .
Thus, if
.
Thus, if 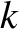 is unconstrained then the fastest growing instability of a
current sheet is such that
is unconstrained then the fastest growing instability of a
current sheet is such that
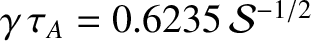 and
and
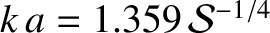 .
.

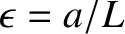 , and
, and 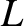 is the periodicity length of the primary magnetic island chain in the
is the periodicity length of the primary magnetic island chain in the 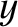 -direction. (Thus, the wavenumber of the island chain is
-direction. (Thus, the wavenumber of the island chain is  .)
Let
us assume that
.)
Let
us assume that
 , as is generally the case in non-constant-
, as is generally the case in non-constant- island chains. Given that
island chains. Given that
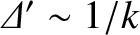 , it follows that
, it follows that
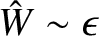 . Hence,
. Hence,
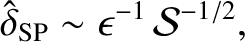
 . We can use the previous analysis to find the fastest growing
instability of the Sweet-Parker current sheet by making the substitutions
. We can use the previous analysis to find the fastest growing
instability of the Sweet-Parker current sheet by making the substitutions
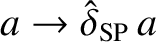 ,
,
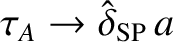 , and
, and
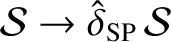 .
Thus, the fastest growing instability has a growth-rate
.
Thus, the fastest growing instability has a growth-rate
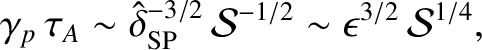
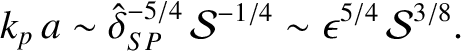
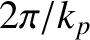 . Thus, the number of plasmoids in the island chain is
. Thus, the number of plasmoids in the island chain is
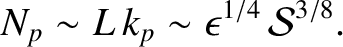
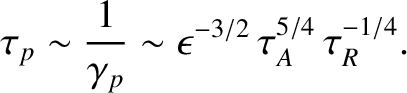

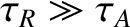 . Note that the normalized thickness of the
secondary Sweet-Parker current sheets that connect the plasmoids is
. Note that the normalized thickness of the
secondary Sweet-Parker current sheets that connect the plasmoids is
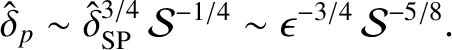
 , and that of
the secondary Sweet-Parker current sheets,
, and that of
the secondary Sweet-Parker current sheets,  . Say,
. Say,

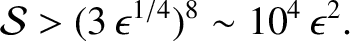
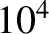 (assuming that
(assuming that
 ). This instability criterion has been verified numerically (Bhattacharjee, et al. 2009).
). This instability criterion has been verified numerically (Bhattacharjee, et al. 2009).