


Next: Homopolar Disk Dynamo
Up: Magnetohydrodynamic Fluids
Previous: Mass and Angular Momentum
MHD Dynamo Theory
Many stars, planets, and galaxies possess magnetic fields whose origins
are not easily explained. Even the ``solid'' planets could not possibly
be sufficiently ferromagnetic to account for their magnetism, because the temperatures of their interiors lie above the Curie temperature at which permanent magnetism
disappears (Reif 1965). It goes without saying that stars and galaxies are not ferromagnetic. Magnetic fields cannot be dismissed as transient
phenomena that just happen to be present today. For instance,
paleomagnetism, the study of magnetic fields ``fossilized'' in rocks
at the time of their formation in the remote geological past, shows
that the Earth's magnetic field has existed at much its present
strength for at least the past
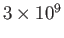 years (Dunlop and Özdemir 2001; Ogg 2012). The problem is that,
in the absence of an internal source of electric currents, magnetic fields contained in a
conducting body decay ohmically on a timescale
years (Dunlop and Özdemir 2001; Ogg 2012). The problem is that,
in the absence of an internal source of electric currents, magnetic fields contained in a
conducting body decay ohmically on a timescale
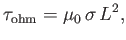 |
(7.100) |
where 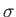 is the typical electrical conductivity, and
is the typical electrical conductivity, and 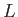 is the
typical lengthscale of the body, and this decay timescale is generally
very small compared to the inferred lifetimes of astrophyiscal magnetic fields. For instance,
the Earth contains a highly conducting region: namely, its molten core, of
radius
is the
typical lengthscale of the body, and this decay timescale is generally
very small compared to the inferred lifetimes of astrophyiscal magnetic fields. For instance,
the Earth contains a highly conducting region: namely, its molten core, of
radius
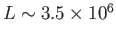 m, and conductivity
m, and conductivity
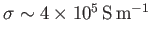 (Yoder 1995). This yields an ohmic decay time for the terrestrial
magnetic field of only
(Yoder 1995). This yields an ohmic decay time for the terrestrial
magnetic field of only
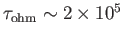 years, which is
obviously far shorter than the inferred lifetime of this field.
Clearly, some process inside the Earth must be actively maintaining the
terrestrial magnetic field (Roberts and King 2013). Such a process is conventionally termed a
dynamo. Similar considerations lead us to postulate the existence
of
dynamos acting inside stars and galaxies, in order to account for the persistence
of stellar and galactic magnetic fields over cosmological timescales (Mestel 2012).
years, which is
obviously far shorter than the inferred lifetime of this field.
Clearly, some process inside the Earth must be actively maintaining the
terrestrial magnetic field (Roberts and King 2013). Such a process is conventionally termed a
dynamo. Similar considerations lead us to postulate the existence
of
dynamos acting inside stars and galaxies, in order to account for the persistence
of stellar and galactic magnetic fields over cosmological timescales (Mestel 2012).
The basic premise of dynamo theory is that all astrophysical bodies that
contain anomalously long-lived magnetic fields also contain convecting, highly conducting,
fluids (e.g., the Earth's molten core, the ionized gas that makes
up the Sun), and it is the electric currents
associated with the motions of these fluids that maintain the
observed magnetic fields. At first sight, this proposal, first
made by Larmor in 1919 (Larmor 1919), sounds suspiciously like
pulling yourself up by your own shoelaces. However, there is really
no conflict with the demands of energy conservation. The
magnetic energy irreversibly
lost via ohmic heating is replenished at the rate
(per unit volume)
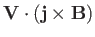 : in other words, by the rate of work done against the
Lorentz force. The flow field,
: in other words, by the rate of work done against the
Lorentz force. The flow field,  , is assumed to be driven via thermal
convention. If the flow is sufficiently vigorous then it is, at least,
plausible that the energy input to the magnetic field can overcome the losses
due to ohmic heating, thus permitting the field to persist over timescales
far longer than the characteristic ohmic decay time.
, is assumed to be driven via thermal
convention. If the flow is sufficiently vigorous then it is, at least,
plausible that the energy input to the magnetic field can overcome the losses
due to ohmic heating, thus permitting the field to persist over timescales
far longer than the characteristic ohmic decay time.
Paleomagnetic data from marine sediment cores shows that the Earth's magnetic
field is quite variable, and actually reversed polarity about  years
ago (Dunlop and Özdemir 2001; Valet, Meynadier, and Guyodo 2005). In fact, more extensive data shows that the Earth's magnetic field
reverses polarity about once every ohmic decay timescale (i.e., a few
times every million years) (Ogg 2012). The Sun's magnetic field exhibits similar
behavior, reversing polarity about once every 11 years (Jones, Thompson, and Tobais 2010; Mestel 2012). An examination of this type of data reveals that dynamo magnetic fields (and velocity fields) are
essentially chaotic
in nature,
exhibiting strong random variability superimposed on more regular quasi-periodic
oscillations.
years
ago (Dunlop and Özdemir 2001; Valet, Meynadier, and Guyodo 2005). In fact, more extensive data shows that the Earth's magnetic field
reverses polarity about once every ohmic decay timescale (i.e., a few
times every million years) (Ogg 2012). The Sun's magnetic field exhibits similar
behavior, reversing polarity about once every 11 years (Jones, Thompson, and Tobais 2010; Mestel 2012). An examination of this type of data reveals that dynamo magnetic fields (and velocity fields) are
essentially chaotic
in nature,
exhibiting strong random variability superimposed on more regular quasi-periodic
oscillations.
A thorough investigation of dynamo
theory would be a far too difficult and time consuming task. Instead, we shall examine a
far simpler version of this theory, known as kinematic dynamo theory, in which
the velocity field,  , is prescribed (Moffatt 1978; Krause and Rädler 1980).
In order for this approach to be self-consistent, it must be assumed that the magnetic field is
sufficiently weak that it does not affect the velocity field.
Let us start from the MHD Ohm's law, modified by resistivity:
, is prescribed (Moffatt 1978; Krause and Rädler 1980).
In order for this approach to be self-consistent, it must be assumed that the magnetic field is
sufficiently weak that it does not affect the velocity field.
Let us start from the MHD Ohm's law, modified by resistivity:
 |
(7.101) |
Here, the resistivity  is assumed to be a constant, for the sake
of simplicity. Taking the curl of the previous equation, and making use
of Maxwell's equations, we obtain
is assumed to be a constant, for the sake
of simplicity. Taking the curl of the previous equation, and making use
of Maxwell's equations, we obtain
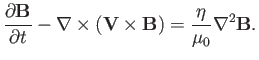 |
(7.102) |
If the velocity field,  , is prescribed, and unaffected by the
presence of the magnetic field, then the previous equation is
essentially a linear eigenvalue equation for the magnetic field,
, is prescribed, and unaffected by the
presence of the magnetic field, then the previous equation is
essentially a linear eigenvalue equation for the magnetic field, 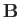 .
The question we wish to address is as follows. For what sort
of velocity fields, if any, does the previous equation possess solutions
in which the magnetic field grows exponentially in time? In trying to formulate an answer to this question,
we hope to learn what type of motion of an MHD fluid is capable of
self-generating
a magnetic field.
.
The question we wish to address is as follows. For what sort
of velocity fields, if any, does the previous equation possess solutions
in which the magnetic field grows exponentially in time? In trying to formulate an answer to this question,
we hope to learn what type of motion of an MHD fluid is capable of
self-generating
a magnetic field.



Next: Homopolar Disk Dynamo
Up: Magnetohydrodynamic Fluids
Previous: Mass and Angular Momentum
Richard Fitzpatrick
2016-01-23
![]() : in other words, by the rate of work done against the
Lorentz force. The flow field,
: in other words, by the rate of work done against the
Lorentz force. The flow field, ![]() , is assumed to be driven via thermal
convention. If the flow is sufficiently vigorous then it is, at least,
plausible that the energy input to the magnetic field can overcome the losses
due to ohmic heating, thus permitting the field to persist over timescales
far longer than the characteristic ohmic decay time.
, is assumed to be driven via thermal
convention. If the flow is sufficiently vigorous then it is, at least,
plausible that the energy input to the magnetic field can overcome the losses
due to ohmic heating, thus permitting the field to persist over timescales
far longer than the characteristic ohmic decay time.
![]() years
ago (Dunlop and Özdemir 2001; Valet, Meynadier, and Guyodo 2005). In fact, more extensive data shows that the Earth's magnetic field
reverses polarity about once every ohmic decay timescale (i.e., a few
times every million years) (Ogg 2012). The Sun's magnetic field exhibits similar
behavior, reversing polarity about once every 11 years (Jones, Thompson, and Tobais 2010; Mestel 2012). An examination of this type of data reveals that dynamo magnetic fields (and velocity fields) are
essentially chaotic
in nature,
exhibiting strong random variability superimposed on more regular quasi-periodic
oscillations.
years
ago (Dunlop and Özdemir 2001; Valet, Meynadier, and Guyodo 2005). In fact, more extensive data shows that the Earth's magnetic field
reverses polarity about once every ohmic decay timescale (i.e., a few
times every million years) (Ogg 2012). The Sun's magnetic field exhibits similar
behavior, reversing polarity about once every 11 years (Jones, Thompson, and Tobais 2010; Mestel 2012). An examination of this type of data reveals that dynamo magnetic fields (and velocity fields) are
essentially chaotic
in nature,
exhibiting strong random variability superimposed on more regular quasi-periodic
oscillations.
![]() , is prescribed (Moffatt 1978; Krause and Rädler 1980).
In order for this approach to be self-consistent, it must be assumed that the magnetic field is
sufficiently weak that it does not affect the velocity field.
Let us start from the MHD Ohm's law, modified by resistivity:
, is prescribed (Moffatt 1978; Krause and Rädler 1980).
In order for this approach to be self-consistent, it must be assumed that the magnetic field is
sufficiently weak that it does not affect the velocity field.
Let us start from the MHD Ohm's law, modified by resistivity: