


Next: MHD Dynamo Theory
Up: Magnetohydrodynamic Fluids
Previous: Interplanetary Magnetic Field
Let us consider what impact the solar wind has on solar evolution. The most obvious question is whether the mass loss due
to the wind is actually significant. Using typical measured values [i.e.,
a typical solar wind velocity and particle density at 1 AU of
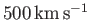 and
and
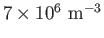 , respectively (Priest 1984)],
the Sun is apparently losing mass at a rate of
, respectively (Priest 1984)],
the Sun is apparently losing mass at a rate of
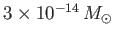 per year, where
per year, where
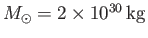 is the solar mass (Yoder 1995), implying a timescale for significant mass loss of
is the solar mass (Yoder 1995), implying a timescale for significant mass loss of
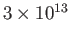 years, or some
years, or some 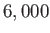 times longer than the estimated
times longer than the estimated
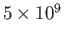 year
age of the Sun (Hansen, Kawaler, and Trimble 2004). Clearly, the mass carried off by the solar wind has a negligible
effect on the Sun's evolution. Note, however, that many stars in the universe
exhibit significant mass loss via stellar winds. This is particularly
the case for late-type stars (Mestel 2012).
year
age of the Sun (Hansen, Kawaler, and Trimble 2004). Clearly, the mass carried off by the solar wind has a negligible
effect on the Sun's evolution. Note, however, that many stars in the universe
exhibit significant mass loss via stellar winds. This is particularly
the case for late-type stars (Mestel 2012).
Let us now consider the angular momentum carried off by the solar wind.
Angular momentum loss is a crucially important topic in astrophysics, because
only by losing angular momentum can large, diffuse objects, such as
interstellar gas clouds, collapse under the influence of gravity to produce
small, compact objects, such as stars and proto-stars (Mestel 2012). Magnetic fields
generally play a crucial role in angular momentum loss. This is certainly
the case for the solar wind, where the solar magnetic field enforces
co-rotation with the Sun out to the Alfvén radius, 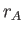 . Thus, the
angular momentum carried away by a particle of mass
. Thus, the
angular momentum carried away by a particle of mass 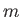 is
is
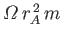 , rather than
, rather than
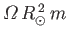 . The angular momentum
loss timescale is, therefore, shorter than the mass loss timescale by a factor
. The angular momentum
loss timescale is, therefore, shorter than the mass loss timescale by a factor
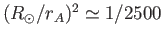 , making the angular momentum loss timescale
comparable to the solar lifetime. It is clear that magnetized stellar
winds represent a very important vehicle for angular momentum loss in the
universe (Mestel 2012). Let us investigate angular momentum loss via
stellar winds in more detail.
, making the angular momentum loss timescale
comparable to the solar lifetime. It is clear that magnetized stellar
winds represent a very important vehicle for angular momentum loss in the
universe (Mestel 2012). Let us investigate angular momentum loss via
stellar winds in more detail.
Under the assumption of spherical symmetry and steady flow, the azimuthal
momentum evolution equation for the solar wind, taking into account the
influence of the interplanetary magnetic field, is written (Huba 2000a)
![$\displaystyle \rho\,[({\bf V}\cdot\nabla){\bf V}]_\phi\equiv \rho\,\frac{u_r}{r...
...({\bf j}\times{\bf B})_\phi \equiv \frac{B_r}{\mu_0\,r}\frac{d(r\,B_\phi)}{dr}.$](img2434.png) |
(7.90) |
The constancy of the mass flux [see Equation (7.64)] and the 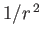 dependence
of
dependence
of 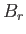 [see Equation (7.83)] permit the immediate integration of the
previous equation to give
[see Equation (7.83)] permit the immediate integration of the
previous equation to give
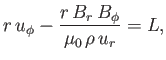 |
(7.91) |
where 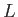 is the angular momentum per unit mass carried off by the solar wind.
In the presence of an azimuthal wind velocity, the magnetic field and
velocity components are related by an expression similar to Equation (7.81):
is the angular momentum per unit mass carried off by the solar wind.
In the presence of an azimuthal wind velocity, the magnetic field and
velocity components are related by an expression similar to Equation (7.81):
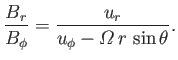 |
(7.92) |
The fundamental physics assumption underlying the previous expression is
the absence of an electric field in the frame of reference co-rotating
with the Sun. Using Equation (7.92) to eliminate 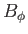 from Equation (7.91), we obtain
(in the ecliptic plane, where
from Equation (7.91), we obtain
(in the ecliptic plane, where
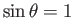 )
)
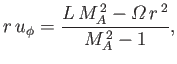 |
(7.93) |
where
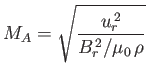 |
(7.94) |
is the radial Alfvén Mach number. The radial Alfvén Mach number
is small near the base of the corona, and about 10 at 1 AU: it passes through
unity at the Alfvén radius, 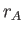 , which is about
, which is about 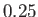 AU from the Sun.
The zero denominator on the right-hand side
of Equation (7.93) at
AU from the Sun.
The zero denominator on the right-hand side
of Equation (7.93) at 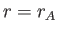 implies that
implies that 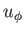 is
finite and continuous only if the numerator is also zero at the Alfvén radius.
This condition then determines the angular momentum content of the outflow
via
is
finite and continuous only if the numerator is also zero at the Alfvén radius.
This condition then determines the angular momentum content of the outflow
via
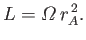 |
(7.95) |
Note that the angular momentum carried off by the solar wind is indeed
equivalent to that which would be carried off were coronal plasma to
co-rotate with the Sun out to the Alfvén radius, and subsequently outflow
at constant angular velocity. Of course, the solar wind does not actually
rotate rigidly with the Sun in the region 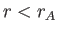 : much of the angular
momentum in this region is carried in the form of electromagnetic stresses.
: much of the angular
momentum in this region is carried in the form of electromagnetic stresses.
It is easily demonstrated that the quantity
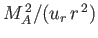 is a constant (because
is a constant (because
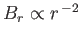 , and
, and
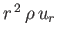 is
constant),
and can, therefore, be evaluated at
is
constant),
and can, therefore, be evaluated at 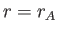 to give
to give
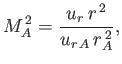 |
(7.96) |
where
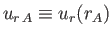 . Equations (7.93), (7.95), and (7.96) can
be combined to produce
. Equations (7.93), (7.95), and (7.96) can
be combined to produce
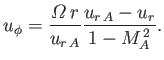 |
(7.97) |
In the limit
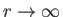 , we have
, we have 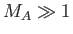 , so the previous
expression yields
, so the previous
expression yields
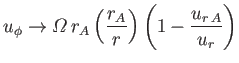 |
(7.98) |
at large distances from the Sun. Recall, from Section 7.7, that if the coronal
plasma were to simply co-rotate with the Sun out to 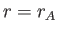 , and experience
no torque beyond this radius, then we would expect
, and experience
no torque beyond this radius, then we would expect
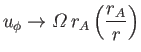 |
(7.99) |
at large distances from the Sun.
The difference between the previous two expressions is the factor
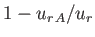 ,
which is a correction for the angular momentum retained by the magnetic
field at large
,
which is a correction for the angular momentum retained by the magnetic
field at large 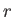 .
.
The previous analysis presented was first incorporated into a quantitative
coronal expansion model by Weber and Davis (Weber and Davis 1967). The model of Weber and Davis is
very complicated. For instance, the solar wind is required to flow smoothly
through no less than three critical points. These are associated
with the sound speed (as in Parker's original model), the radial Alfvén
speed,
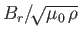 , (as previously described), and the total
Alfvén speed,
, (as previously described), and the total
Alfvén speed,
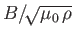 .
Nevertheless, the simplified analysis
outlined in this section captures most of the essential features of the outflow.
.
Nevertheless, the simplified analysis
outlined in this section captures most of the essential features of the outflow.



Next: MHD Dynamo Theory
Up: Magnetohydrodynamic Fluids
Previous: Interplanetary Magnetic Field
Richard Fitzpatrick
2016-01-23
![]() . Thus, the
angular momentum carried away by a particle of mass
. Thus, the
angular momentum carried away by a particle of mass ![]() is
is
![]() , rather than
, rather than
![]() . The angular momentum
loss timescale is, therefore, shorter than the mass loss timescale by a factor
. The angular momentum
loss timescale is, therefore, shorter than the mass loss timescale by a factor
![]() , making the angular momentum loss timescale
comparable to the solar lifetime. It is clear that magnetized stellar
winds represent a very important vehicle for angular momentum loss in the
universe (Mestel 2012). Let us investigate angular momentum loss via
stellar winds in more detail.
, making the angular momentum loss timescale
comparable to the solar lifetime. It is clear that magnetized stellar
winds represent a very important vehicle for angular momentum loss in the
universe (Mestel 2012). Let us investigate angular momentum loss via
stellar winds in more detail.
![$\displaystyle \rho\,[({\bf V}\cdot\nabla){\bf V}]_\phi\equiv \rho\,\frac{u_r}{r...
...({\bf j}\times{\bf B})_\phi \equiv \frac{B_r}{\mu_0\,r}\frac{d(r\,B_\phi)}{dr}.$](img2434.png)
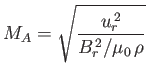
![]() is a constant (because
is a constant (because
![]() , and
, and
![]() is
constant),
and can, therefore, be evaluated at
is
constant),
and can, therefore, be evaluated at ![]() to give
to give
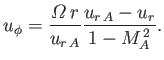
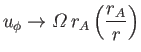
![]() , (as previously described), and the total
Alfvén speed,
, (as previously described), and the total
Alfvén speed,
![]() .
Nevertheless, the simplified analysis
outlined in this section captures most of the essential features of the outflow.
.
Nevertheless, the simplified analysis
outlined in this section captures most of the essential features of the outflow.