The hot coronal plasma making up the solar wind possesses an extremely high electrical conductivity. In such a plasma, we expect the concept of ``frozen-in'' magnetic field-lines, discussed in Section 7.3, to be applicable. The continuous flow of coronal material into interplanetary space must, therefore, result in the transport of the solar magnetic field into the interplanetary region. If the Sun did not rotate then the resulting magnetic configuration would be very simple. The radial coronal expansion considered previously (with the neglect of any magnetic forces) would produce magnetic field-lines extending radially outward from the Sun.
Of course, the Sun does rotate, with a (latitude dependent) period of
about 25 days.7.1 Because the solar photosphere is an
excellent electrical conductor, the magnetic field at the base of the
corona is frozen into the rotating frame of reference of the Sun.
A magnetic field-line starting from a given location on the surface of the Sun is
drawn out along the path followed by the element of the solar
wind emanating from that location. As before, let us suppose that the coronal expansion is
purely radial in a stationary frame of reference.
Consider a spherical
coordinate system
![]() that co-rotates with the Sun.
Of course, the symmetry axis of the coordinate system is assumed to coincide
with the axis of the Sun's rotation. In the rotating coordinate system,
the velocity components of the solar wind are written
that co-rotates with the Sun.
Of course, the symmetry axis of the coordinate system is assumed to coincide
with the axis of the Sun's rotation. In the rotating coordinate system,
the velocity components of the solar wind are written
| (7.78) | ||
| (7.79) | ||
| (7.80) |
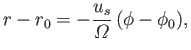 |
(7.82) |
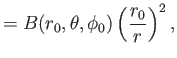 |
(7.83) | |
| (7.84) | ||
 |
(7.85) |
Figure 7.4 illustrates the interplanetary magnetic field close to the
ecliptic plane (i.e.,
![]() ). The magnetic field-lines of the Sun are drawn into Archimedean spirals
by the solar rotation. Transformation
to a stationary frame of reference gives the same magnetic field configuration,
with the addition of an electric field
). The magnetic field-lines of the Sun are drawn into Archimedean spirals
by the solar rotation. Transformation
to a stationary frame of reference gives the same magnetic field configuration,
with the addition of an electric field
| (7.86) |
The interplanetary magnetic field at 1 AU is observed to lie in the
ecliptic plane, and is directed at an angle of approximately ![]() from
the radial direction to the Sun (Priest 1984). This is in basic agreement with the spiral
configuration predicted previously.
from
the radial direction to the Sun (Priest 1984). This is in basic agreement with the spiral
configuration predicted previously.
The previous analysis is premised on the assumption that the
interplanetary magnetic field is too weak to affect the coronal outflow, and
is, therefore, passively convected by the solar wind. In fact, this is only
the case if the interplanetary
magnetic energy density,
![]() , is
much less that the kinetic energy density,
, is
much less that the kinetic energy density,
![]() , of the solar wind.
Rearrangement yields the condition
, of the solar wind.
Rearrangement yields the condition
| (7.87) |
Well inside the Alfvén radius (i.e., in the region ![]() ),
the solar wind is too weak to modify the structure of the solar magnetic field.
In fact, in this region, we expect the solar magnetic field to
force the solar wind to
co-rotate with the Sun. Observe that flux-freezing is a two-way-street:
if the energy density of the flow greatly exceeds that of the magnetic field
then the magnetic field is passively convected by the flow, but if
the energy density of the magnetic field greatly exceeds that of the flow
then the flow is forced to conform to the magnetic field.
),
the solar wind is too weak to modify the structure of the solar magnetic field.
In fact, in this region, we expect the solar magnetic field to
force the solar wind to
co-rotate with the Sun. Observe that flux-freezing is a two-way-street:
if the energy density of the flow greatly exceeds that of the magnetic field
then the magnetic field is passively convected by the flow, but if
the energy density of the magnetic field greatly exceeds that of the flow
then the flow is forced to conform to the magnetic field.
The previous discussion leads us to the following, rather crude, picture of the
interaction of the solar wind and the interplanetary magnetic field.
We expect the interplanetary
magnetic field to be the undistorted continuation of
the Sun's magnetic field for ![]() . On the other hand, we
expect the interplanetary field to be dragged out into a spiral
pattern for
. On the other hand, we
expect the interplanetary field to be dragged out into a spiral
pattern for ![]() . Furthermore, we expect the Sun's magnetic field
to impart a non-zero azimuthal velocity
. Furthermore, we expect the Sun's magnetic field
to impart a non-zero azimuthal velocity ![]() to the solar
wind. In the ecliptic plane (
to the solar
wind. In the ecliptic plane (
![]() ), we infer that
), we infer that
| (7.88) |
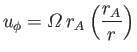 |
(7.89) |