


Next: Bibliography
Up: Waves in Warm Plasmas
Previous: Harris Instability
- Derive the dispersion relation (8.28) from Equations (8.23)-(8.27).
- Show that the dispersion relation (8.28) can be written
where
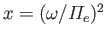 ,
,
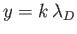 ,
,
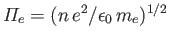 ,
,
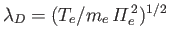 , and
, and
Demonstrate that, in the limit 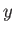 ,
,
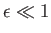 , the approximate solution is
, the approximate solution is
- Show that, when combined with the Maxwellian velocity distribution (8.24), the dispersion relation (8.23) reduces to
where
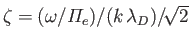 ,
,
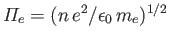 ,
,
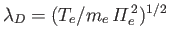 , and
, and 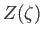 is the plasma dispersion function.
Hence, deduce from the large argument asymptotic form of the plasma dispersion function that
is the plasma dispersion function.
Hence, deduce from the large argument asymptotic form of the plasma dispersion function that
in the limit
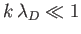 . Show that the approximate solution of the previous equation is
. Show that the approximate solution of the previous equation is
- Show that, when combined with the Maxwellian velocity distribution (8.24), the dispersion relation (8.49) reduces to
where
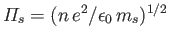 ,
,
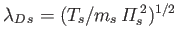 ,
,
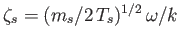 , and
, and 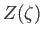 is the plasma dispersion
function.
Use the large-argument expansion of the plasma dispersion function for the ions,
is the plasma dispersion
function.
Use the large-argument expansion of the plasma dispersion function for the ions,
and the small-argument expansion for the electrons,
Substituting these expansions into the
dispersion relation, writing
 , where
, where 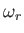 and
and  are both real,
and
are both real,
and
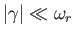 , demonstrate that
, demonstrate that
and
- Derive Equation (8.74) from Equations (8.69) and (8.73).
- Derive Equation (8.82) from Equations (8.74) and (8.79).
- Derive Equations (8.89)-(8.91) from Equation (8.82).
- Derive Equations (8.94)-(8.96) from Equation (8.82).
- Derive Equations (8.102)-(8.105) from Equation (8.82).
- Derive Equation (8.119) from Equation (8.118).
- Derive Equation (8.120) from Equations (8.79) and (8.119).
- Derive Equation (8.124) from Equation (8.123).
- Demonstrate that the distribution function (8.131) possesses a minimum at
 when
when
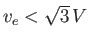 , but not otherwise.
, but not otherwise.
- Verify formula (8.133).
- Consider an unmagnetized quasi-neutral plasma with stationary ions in which the electron velocity
distribution function takes the form
Demonstrate that the dispersion relation for electrostatic plasma waves can be written
where
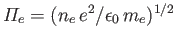 . Assuming that
. Assuming that 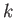 is real and positive, and that
is real and positive, and that 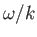 lies in the upper half of the complex plane, show
that when the integrals are evaluated as contour integrals in the complex
lies in the upper half of the complex plane, show
that when the integrals are evaluated as contour integrals in the complex 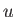 -plane (closed in the lower half of the plane), making use of the residue theorem (Riley 1974), the previous dispersion relation reduces to
-plane (closed in the lower half of the plane), making use of the residue theorem (Riley 1974), the previous dispersion relation reduces to
where
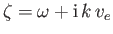 . Finally, in the small-
. Finally, in the small-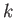 limit,
limit,
 , demonstrate that the growth-rate of the most unstable mode
is
, demonstrate that the growth-rate of the most unstable mode
is
- Derive Equation (8.137) from Equations (8.134)-(8.136).
- Derive Equations (8.160) and (8.161) from Equations (8.154), (8.155), and (8.159).



Next: Bibliography
Up: Waves in Warm Plasmas
Previous: Harris Instability
Richard Fitzpatrick
2016-01-23
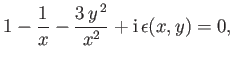
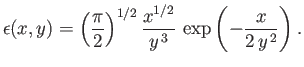
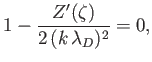
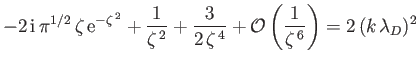
![$\displaystyle \frac{\omega}{{\mit\Pi}_e}= \sqrt{2}\,(k\,\lambda_D)\,\zeta \sime...
...1/2}\frac{1}{(k\,\lambda_D)^3}\exp\left[-\frac{1}{2\,(k\,\lambda_D)^2}\right].
$](img3456.png)
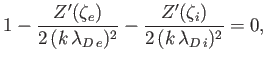
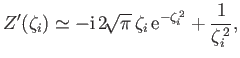
![$\displaystyle \frac{\omega_r}{k} \simeq \left(\frac{T_e}{m_i}\right)^{1/2}\frac{1}{\left[1+(k\,\lambda_{D\,e})^{2}\right]^{1/2}},
$](img3461.png)
![$\displaystyle \frac{\gamma}{\omega_r} \simeq -\frac{(\pi/8)^{1/2}}{\left[1+(k\,...
...ac{T_e}{2\,T_i}\,\frac{1}{\left[1+(k\,\lambda_{D\,e})^2\right]}\right)\right].
$](img3462.png)
![$\displaystyle F_0(u) = n_e\,\frac{v_e}{2\pi}\left[\frac{1}{v_e^{\,2}+(u-V)^{\,2}} + \frac{1}{v_e^{\,2}+(u+V)^{\,2}}\right].$](img3342.png)
![$\displaystyle = {\mit\Pi}_e^{\,2}\,\frac{v_e}{2\pi}\left[\int_{-\infty}^\infty \frac{du}{(u-\omega/k)^2\,[v_e^{\,2} + (u-V)^{\,2}]} \right.$](img3463.png)
![$\displaystyle \phantom{{\mit\Pi}_e^{\,2}\,\frac{v_e}{2\pi}====}\left.+ \int_{-\infty}^\infty \frac{du}{(u-\omega/k)^2\,[v_e^{\,2} + (u+V)^{\,2}]} \right],$](img3464.png)
![$\displaystyle 2 = {\mit\Pi}_e^{\,2}\left[\frac{1}{(k\,V - \zeta)^{\,2}}+ \frac{1}{(k\,V+\zeta)^{\,2}}\right],
$](img3465.png)