


Next: Electrostatic Waves
Up: Waves in Warm Plasmas
Previous: Parallel Wave Propagation
Let us now consider wave propagation, through a warm plasma, perpendicular
to the equilibrium magnetic field. For perpendicular propagation,
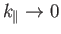 ,
and, hence, from Equation (8.85),
,
and, hence, from Equation (8.85),
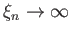 . Making use of
the asymptotic expansions (8.86) and (8.87), the matrix
. Making use of
the asymptotic expansions (8.86) and (8.87), the matrix 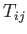 simplifies
considerably. The dispersion relation can again be written
in the form (8.93), where
simplifies
considerably. The dispersion relation can again be written
in the form (8.93), where
and
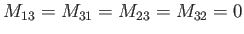 .
Here,
.
Here,
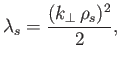 |
(8.106) |
where
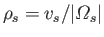 is the species-
is the species-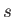 gyroradius.
gyroradius.
The first root of the dispersion relation (8.93) is
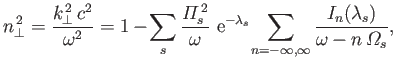 |
(8.107) |
with the eigenvector
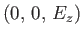 . This dispersion relation obviously
corresponds to the electromagnetic plasma wave, or ordinary mode, discussed
in Section 5.10.
However, in a warm plasma, the dispersion relation for the ordinary mode
is strongly modified by the introduction of resonances (where the refractive
index,
. This dispersion relation obviously
corresponds to the electromagnetic plasma wave, or ordinary mode, discussed
in Section 5.10.
However, in a warm plasma, the dispersion relation for the ordinary mode
is strongly modified by the introduction of resonances (where the refractive
index, 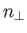 ,
becomes infinite) at all the harmonics of the cyclotron frequencies:
,
becomes infinite) at all the harmonics of the cyclotron frequencies:
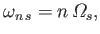 |
(8.108) |
where 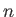 is a non-zero integer. These resonances are a finite gyroradius
effect. In fact, they originate from the variation of the wave phase
across a gyro-orbit (Cairns 1985). Thus, in the cold plasma limit,
is a non-zero integer. These resonances are a finite gyroradius
effect. In fact, they originate from the variation of the wave phase
across a gyro-orbit (Cairns 1985). Thus, in the cold plasma limit,
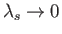 ,
in which the gyroradii shrink to zero, all of the resonances disappear from
the dispersion relation. In the limit in which the wavelength,
,
in which the gyroradii shrink to zero, all of the resonances disappear from
the dispersion relation. In the limit in which the wavelength, 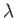 , of
the wave is much larger than a typical gyroradius,
, of
the wave is much larger than a typical gyroradius, 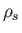 , the
relative amplitude of the
, the
relative amplitude of the 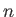 th harmonic cyclotron resonance, as it
appears in the dispersion
relation (8.107), is approximately
th harmonic cyclotron resonance, as it
appears in the dispersion
relation (8.107), is approximately
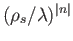 [see Equations (8.88) and (8.106)]. It is clear, therefore, that,
in this limit, only low-order resonances [i.e.,
[see Equations (8.88) and (8.106)]. It is clear, therefore, that,
in this limit, only low-order resonances [i.e.,
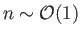 ] couple
strongly into the dispersion relation, and high-order resonances
(i.e.,
] couple
strongly into the dispersion relation, and high-order resonances
(i.e., 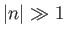 ) can effectively be neglected. As
) can effectively be neglected. As
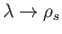 , the high-order resonances become increasingly important, until,
when
, the high-order resonances become increasingly important, until,
when
 , all of the resonances are of approximately equal
strength. Because the ion gyroradius is generally much larger than the
electron gyroradius, it follows that the ion cyclotron harmonic resonances
are generally more important than the electron cyclotron harmonic resonances.
, all of the resonances are of approximately equal
strength. Because the ion gyroradius is generally much larger than the
electron gyroradius, it follows that the ion cyclotron harmonic resonances
are generally more important than the electron cyclotron harmonic resonances.
Observe that the cyclotron harmonic resonances appearing in the dispersion
relation (8.107) are of zero width in frequency space: that is, they are
just like the resonances that appear in the cold-plasma limit.
Actually, this is just an artifact of the fact that the waves we are studying
propagate exactly perpendicular to the equilibrium magnetic field. It is
clear, from an examination of Equations (8.83) and (8.85), that the cyclotron
harmonic resonances originate from the zeros of the plasma dispersion
functions. Adopting the usual rule that substantial damping takes place
whenever the arguments of the dispersion functions are less than or of
order unity, it follows that the cyclotron harmonic resonances lead to
significant damping whenever
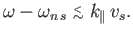 |
(8.109) |
Thus, the cyclotron harmonic resonances possess a finite width in frequency
space provided the parallel wavenumber,
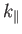 , is non-zero: that is,
provided the wave does not propagate exactly perpendicular to the magnetic
field.
, is non-zero: that is,
provided the wave does not propagate exactly perpendicular to the magnetic
field.
The appearance of the cyclotron harmonic resonances in a warm plasma
is of great practical
importance in plasma physics, because it greatly increases the number of
resonant frequencies at which waves can transfer energy to the
plasma. In magnetic fusion experiments, these resonances are routinely exploited to
heat plasmas via externally launched electromagnetic waves (Stix 1992; Swanson 2003).
Figure:
Dispersion relation for electron Bernstein waves in a warm plasma for which
 .
.
 |
The other roots of the dispersion relation (8.93) satisfy
with the eigenvector
 . In the cold plasma limit,
. In the cold plasma limit,
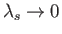 , this dispersion relation reduces to that of the extraordinary mode
discussed in Section 5.10. This mode, for which
, this dispersion relation reduces to that of the extraordinary mode
discussed in Section 5.10. This mode, for which
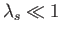 , unless the
plasma possesses a thermal velocity approaching the velocity of light, is little
affected by thermal effects, except close to the cyclotron harmonic
resonances,
, unless the
plasma possesses a thermal velocity approaching the velocity of light, is little
affected by thermal effects, except close to the cyclotron harmonic
resonances,
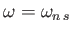 , where small thermal corrections are important
because of the smallness of the denominators in the previous dispersion relation (Cairns 1985).
, where small thermal corrections are important
because of the smallness of the denominators in the previous dispersion relation (Cairns 1985).
However, another mode also exists. In fact, if we look for a mode with a
phase-velocity much less than the velocity of light (i.e.,
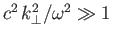 ) then it is clear from (8.102)-(8.105) that
the dispersion relation is approximately
) then it is clear from (8.102)-(8.105) that
the dispersion relation is approximately
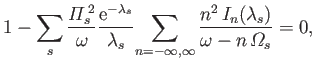 |
(8.111) |
and the associated eigenvector is
 . The new waves, which
are called Bernstein waves--after I.B. Bernstein, who first
discovered them (Bernstein 1958)--are a type of slowly propagating,
longitudinal, electrostatic wave.
. The new waves, which
are called Bernstein waves--after I.B. Bernstein, who first
discovered them (Bernstein 1958)--are a type of slowly propagating,
longitudinal, electrostatic wave.
Let us consider electron Bernstein waves, for the sake of definiteness.
Neglecting the contribution of the ions, which is reasonable provided that
the wave frequencies are sufficiently high, the dispersion relation (8.111)
reduces to
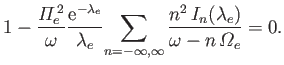 |
(8.112) |
In the limit
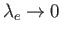 (with
(with
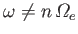 ), only the
), only the 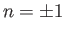 terms survive in the
previous expression. [See Equation (8.88).] In fact, because
terms survive in the
previous expression. [See Equation (8.88).] In fact, because
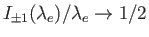 as
as
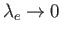 , the dispersion relation yields
, the dispersion relation yields
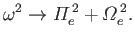 |
(8.113) |
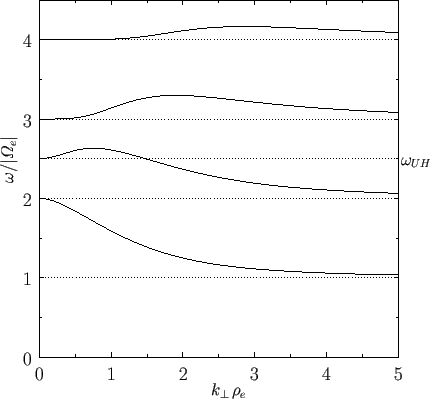
It follows that there is a Bernstein wave whose frequency asymptotes
to the upper hybrid frequency (see Section 5.10) in the limit
 . For other non-zero values of
. For other non-zero values of 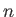 , we have
, we have
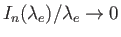 as
as
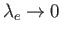 . However, a solution to Equation (8.111) can
be obtained if
. However, a solution to Equation (8.111) can
be obtained if
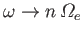 at the same time. Similarly,
as
at the same time. Similarly,
as
 , we have
, we have
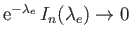 (Abramowitz and Stegun 1965c). In this case, a solution can only be obtained if
(Abramowitz and Stegun 1965c). In this case, a solution can only be obtained if
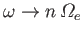 , for some
, for some 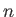 , at the same time. The complete solution to
Equation (8.111) is plotted in Figure 8.8 for a case where the upper
hybrid frequency lies between
, at the same time. The complete solution to
Equation (8.111) is plotted in Figure 8.8 for a case where the upper
hybrid frequency lies between
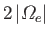 and
and
 .
In fact, wherever the upper hybrid frequency lies, the Bernstein modes above
and below it behave like those shown in the diagram.
.
In fact, wherever the upper hybrid frequency lies, the Bernstein modes above
and below it behave like those shown in the diagram.
At small values of 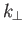 , the phase-velocity becomes large, and
it is no longer legitimate to neglect the extraordinary mode (Cairns 1985). A more detailed
examination of the complete dispersion relation shows that the extraordinary mode
and the Bernstein mode cross over near the harmonics of the cyclotron frequency
to give the pattern shown in Figure 8.9. Here, the dashed line shows the cold
plasma extraordinary mode.
, the phase-velocity becomes large, and
it is no longer legitimate to neglect the extraordinary mode (Cairns 1985). A more detailed
examination of the complete dispersion relation shows that the extraordinary mode
and the Bernstein mode cross over near the harmonics of the cyclotron frequency
to give the pattern shown in Figure 8.9. Here, the dashed line shows the cold
plasma extraordinary mode.
Figure:
Dispersion relation for extraordinary/electron Bernstein waves in a warm plasma for which
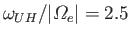 and
and
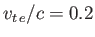 . The dashed
line indicates the cold plasma extraordinary mode.
. The dashed
line indicates the cold plasma extraordinary mode.
 |
In a lower frequency range, a similar phenomena occurs at the
harmonics of the ion cyclotron frequency, producing ion Bernstein waves, with
somewhat similar properties to electron Bernstein waves. Note, however, that
while the ion contribution to the dispersion relation can be neglected for
high-frequency waves, the electron contribution cannot be neglected
for low-frequency waves, so there is not a complete symmetry between the
two types of Bernstein waves.



Next: Electrostatic Waves
Up: Waves in Warm Plasmas
Previous: Parallel Wave Propagation
Richard Fitzpatrick
2016-01-23

![$\displaystyle = -M_{21} =- {\rm i}\sum_s \frac{{\mit\Pi}_s^{\,2}}{\omega} \,\,{...
...rac{n\,\left[I_n'(\lambda_s) -I_n(\lambda_s)\right]}{\omega-n\,{\mit\Omega}_s},$](img3254.png)
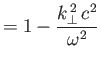
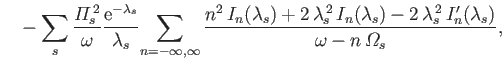

![$\displaystyle = -M_{21} =- {\rm i}\sum_s \frac{{\mit\Pi}_s^{\,2}}{\omega} \,\,{...
...rac{n\,\left[I_n'(\lambda_s) -I_n(\lambda_s)\right]}{\omega-n\,{\mit\Omega}_s},$](img3254.png)
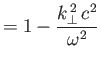
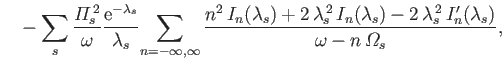
![]() ) then it is clear from (8.102)-(8.105) that
the dispersion relation is approximately
) then it is clear from (8.102)-(8.105) that
the dispersion relation is approximately
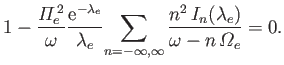
![]() , the phase-velocity becomes large, and
it is no longer legitimate to neglect the extraordinary mode (Cairns 1985). A more detailed
examination of the complete dispersion relation shows that the extraordinary mode
and the Bernstein mode cross over near the harmonics of the cyclotron frequency
to give the pattern shown in Figure 8.9. Here, the dashed line shows the cold
plasma extraordinary mode.
, the phase-velocity becomes large, and
it is no longer legitimate to neglect the extraordinary mode (Cairns 1985). A more detailed
examination of the complete dispersion relation shows that the extraordinary mode
and the Bernstein mode cross over near the harmonics of the cyclotron frequency
to give the pattern shown in Figure 8.9. Here, the dashed line shows the cold
plasma extraordinary mode.
