Next: Current-Driven Ion Acoustic Instability
Up: Waves in Warm Plasmas
Previous: Velocity-Space Instabilities
Counter-Propagating Beam Instability
As an example of a potentially unstable velocity distribution function, consider
![$\displaystyle F_0(u) = n_e\,\frac{v_e}{2\pi}\left[\frac{1}{v_e^{\,2}+(u-V)^{\,2}} + \frac{1}{v_e^{\,2}+(u+V)^{\,2}}\right].$](img3342.png) |
(8.131) |
This function corresponds to two counter-streaming electron beams with so-called Cauchy velocity distributions characterized by the mean velocities 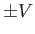 , and the thermal
spreads
, and the thermal
spreads 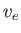 . Here,
. Here,
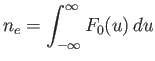 |
(8.132) |
is the electron number density. (It is assumed that there is a stationary background ion fluid of charge density 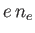 .)
We have seen that a necessary, but not sufficient, criterion for the distribution function (8.131)
to be unstable is that it should possess a minimum at finite
.)
We have seen that a necessary, but not sufficient, criterion for the distribution function (8.131)
to be unstable is that it should possess a minimum at finite 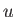 . It is easily demonstrated that this is the case provided
. It is easily demonstrated that this is the case provided
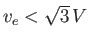 , and, furthermore, that the minimum lies at
, and, furthermore, that the minimum lies at
 . Thus, the system is potentially unstable if
. Thus, the system is potentially unstable if
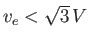 . In order to determine whether the system is actually
unstable, we need to evaluate the Penrose condition (8.130) at the minimum. It turns out that the Penrose integral can be evaluated exactly for
. In order to determine whether the system is actually
unstable, we need to evaluate the Penrose condition (8.130) at the minimum. It turns out that the Penrose integral can be evaluated exactly for
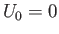 . In fact,
. In fact,
![$\displaystyle \int_{-\infty}^\infty \frac{F_0(u)-F_0(U_0)}{(u-U_0)^{\,2}}\,du = n_e\left[\frac{V^{\,2}- v_e^{\,2}}{(V^{\,2}+ v_e^{\,2})^{\,2}}\right].$](img3349.png) |
(8.133) |
The instability criterion is that this integral be positive, which yields 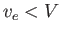 . Assuming that
. Assuming that 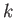 is real and positive, it can be shown that, in the small-
is real and positive, it can be shown that, in the small-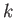 limit,
limit,
 , the growth-rate of the instability is written
, the growth-rate of the instability is written
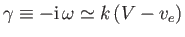 .
.



Next: Current-Driven Ion Acoustic Instability
Up: Waves in Warm Plasmas
Previous: Velocity-Space Instabilities
Richard Fitzpatrick
2016-01-23
![$\displaystyle F_0(u) = n_e\,\frac{v_e}{2\pi}\left[\frac{1}{v_e^{\,2}+(u-V)^{\,2}} + \frac{1}{v_e^{\,2}+(u+V)^{\,2}}\right].$](img3342.png)