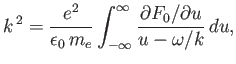 |
(8.125) |
Consider the dispersion relation (8.23) for an electrostatic plasma wave in an unmagnetized quasi-neutral plasma with stationary ions. This relation can be written
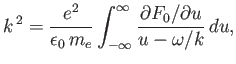 |
(8.125) |
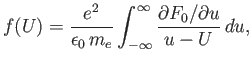 |
(8.127) |
To answer the previous question, we employ a standard result in complex variable theory which states that
the number of zeros minus the number of poles of
![]() in a given region of the complex
in a given region of the complex ![]() plane
is
plane
is
![]() times the increase in the argument of
times the increase in the argument of
![]() as
as ![]() moves once counter-clockwise
around the boundary of this region (Flanigan 2010). To determine the latter quantity, we construct
what is known as a Nyquist diagram (Nyquist 1932). Because the region in which we are interested is the
upper-half complex plane, we let
moves once counter-clockwise
around the boundary of this region (Flanigan 2010). To determine the latter quantity, we construct
what is known as a Nyquist diagram (Nyquist 1932). Because the region in which we are interested is the
upper-half complex plane, we let ![]() follow the semi-circular path shown in Figure 8.10(a), and
plot the corresponding path followed in the complex plane by
follow the semi-circular path shown in Figure 8.10(a), and
plot the corresponding path followed in the complex plane by ![]() , as illustrated in Figure 8.10(b).
Now,
, as illustrated in Figure 8.10(b).
Now,
![]() as
as
![]() . Hence, if the radius of the semicircle in Figure 8.10(a)
tends to infinity, then only that part of the contour running along the real axis is important, and the
. Hence, if the radius of the semicircle in Figure 8.10(a)
tends to infinity, then only that part of the contour running along the real axis is important, and the ![]() contour
starts and finishes at the origin. Because the function
contour
starts and finishes at the origin. Because the function ![]() is analytic in the upper-half
is analytic in the upper-half ![]() plane, by virtue of the way
in which it is defined, the number of zeros of
plane, by virtue of the way
in which it is defined, the number of zeros of
![]() is equal to the change in argument (divided by
is equal to the change in argument (divided by ![]() ) of this
quantity as the path shown in Figure 8.10(b) is followed. However, this is just the number of times that the path
encircles the point
) of this
quantity as the path shown in Figure 8.10(b) is followed. However, this is just the number of times that the path
encircles the point ![]() . Hence, the criterion for instability is that the path should encircle part of the positive real axis.
Thus, in Figure 8.10(b), the system is unstable for the indicated values of
. Hence, the criterion for instability is that the path should encircle part of the positive real axis.
Thus, in Figure 8.10(b), the system is unstable for the indicated values of ![]() (Cairns 1985).
(Cairns 1985).
In an unstable system, there must exist a point such as ![]() in Figure 8.10(b) where the
in Figure 8.10(b) where the ![]() contour
crosses the real axis going from negative to positive imaginary part. Now, as
contour
crosses the real axis going from negative to positive imaginary part. Now, as
![]() moves along the real axis [cf., Equation (8.26)],
moves along the real axis [cf., Equation (8.26)],
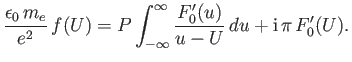 |
(8.128) |
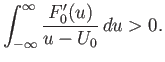 |
(8.129) |
The previous discussion implies that a single-humped velocity distribution function, such as a Maxwellian, is absolutely stable to
velocity-space instabilities (Gardner 1963). This follows because there is no finite value of ![]() at which such a distribution function
attains a minimum value. In fact, assuming that the distribution function,
at which such a distribution function
attains a minimum value. In fact, assuming that the distribution function, ![]() , is such that
, is such that
![]() as
as
![]() , we deduce that an unstable distribution function must possess at least
one minimum and two maxima for
, we deduce that an unstable distribution function must possess at least
one minimum and two maxima for ![]() in the range
in the range
![]() .
.