


Next: Fast Magnetic Reconnection
Up: Magnetohydrodynamic Fluids
Previous: Linear Tearing Mode Theory
Nonlinear Tearing Mode Theory
We have seen that if
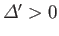 then a magnetic field configuration
of the type shown in Figure 7.7 is unstable to a tearing mode.
Let us now investigate how a tearing instability affects the field
configuration as it develops.
then a magnetic field configuration
of the type shown in Figure 7.7 is unstable to a tearing mode.
Let us now investigate how a tearing instability affects the field
configuration as it develops.
It is convenient to write the magnetic field in terms of a flux-function:
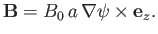 |
(7.217) |
Note that
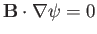 . It follows that magnetic field-lines
run along contours of
. It follows that magnetic field-lines
run along contours of 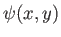 .
.
We can write
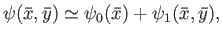 |
(7.218) |
where 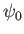 generates the equilibrium magnetic field, and
generates the equilibrium magnetic field, and 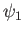 generates
the perturbed magnetic field associated with the tearing mode.
Here,
generates
the perturbed magnetic field associated with the tearing mode.
Here,
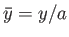 .
In the vicinity of the interface, we have
.
In the vicinity of the interface, we have
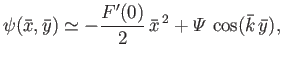 |
(7.219) |
where
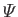 is a constant. Here, we have made use of the
fact that
is a constant. Here, we have made use of the
fact that
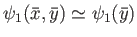 if the
constant-
if the
constant-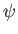 approximation holds good (which is assumed to be the case).
approximation holds good (which is assumed to be the case).
Let
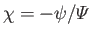 and
and
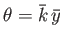 .
It follows that the normalized perturbed magnetic flux function,
.
It follows that the normalized perturbed magnetic flux function, 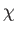 ,
in the vicinity of the interface takes the form
,
in the vicinity of the interface takes the form
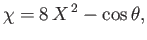 |
(7.220) |
where
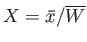 , and
, and
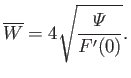 |
(7.221) |
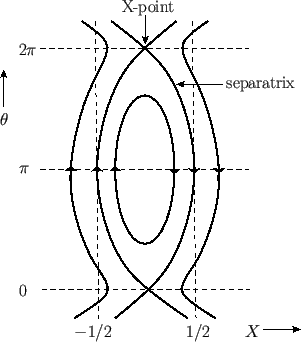
Figure 7.8 shows the contours of 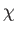 plotted in
plotted in 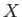 -
-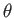 space. It can
be seen that the tearing mode gives rise to
the formation of a magnetic island centered on the interface,
space. It can
be seen that the tearing mode gives rise to
the formation of a magnetic island centered on the interface, 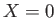 .
Magnetic field-lines situated outside the ``separatrix'' are displaced by the
tearing mode, but still retain their original topology. By contrast, field-lines
inside the separatrix have been broken and reconnected, and now possess
quite different topology. The reconnection obviously takes place at the ``X-points,''
which are located at
.
Magnetic field-lines situated outside the ``separatrix'' are displaced by the
tearing mode, but still retain their original topology. By contrast, field-lines
inside the separatrix have been broken and reconnected, and now possess
quite different topology. The reconnection obviously takes place at the ``X-points,''
which are located at 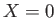 and
and
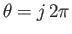 , where
, where 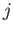 is an integer.
The maximum width of the reconnected region (in
is an integer.
The maximum width of the reconnected region (in 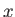 -space) is given by
the island width,
-space) is given by
the island width,
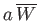 . Note that the island width is proportional
to the square root of the perturbed ``radial'' magnetic field at the interface
(i.e.,
. Note that the island width is proportional
to the square root of the perturbed ``radial'' magnetic field at the interface
(i.e.,
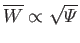 ).
).
Figure 7.8:
Magnetic field-lines in the vicinity of a magnetic island.
 |
According to a result first established in a very elegant paper by
Rutherford (Rutherford 1973),
the nonlinear evolution of the island width is governed by
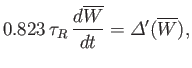 |
(7.222) |
where
![$\displaystyle {\mit\Delta}'(\overline{W}) = \left[\frac{1}{\psi}\frac{d\psi}{d\bar{x}}\right]_{-\overline{W}/2}^{+\overline{W}/2}$](img2767.png) |
(7.223) |
is the jump in the logarithmic derivative of 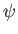 taken across the island (White, Monticello, Rosenbluth, and Waddell 1977).
It is clear that once the tearing mode enters the nonlinear regime (i.e.,
once the normalized island width,
taken across the island (White, Monticello, Rosenbluth, and Waddell 1977).
It is clear that once the tearing mode enters the nonlinear regime (i.e.,
once the normalized island width,
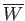 , exceeds the normalized linear layer width,
, exceeds the normalized linear layer width, 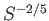 ),
the growth-rate of the instability slows down considerably, until the mode
eventually ends up growing on the extremely slow resistive timescale,
),
the growth-rate of the instability slows down considerably, until the mode
eventually ends up growing on the extremely slow resistive timescale, 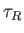 .
The tearing mode stops growing when it has attained a saturated island width
.
The tearing mode stops growing when it has attained a saturated island width
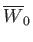 , satisfying
, satisfying
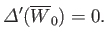 |
(7.224) |
The saturated width is a function of the original
plasma equilibrium, but is independent
of the resistivity. There is no particular reason why
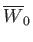 should
be small. In general, the saturated island width is comparable
with the characteristic lengthscale of the magnetic field configuration.
We conclude that, although ideal-MHD only breaks down in a narrow region of relative
width
should
be small. In general, the saturated island width is comparable
with the characteristic lengthscale of the magnetic field configuration.
We conclude that, although ideal-MHD only breaks down in a narrow region of relative
width 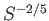 , centered on the interface,
, centered on the interface,  , the reconnection of
magnetic field-lines that takes place
in this region is capable of significantly
modifying the whole magnetic field configuration.
, the reconnection of
magnetic field-lines that takes place
in this region is capable of significantly
modifying the whole magnetic field configuration.



Next: Fast Magnetic Reconnection
Up: Magnetohydrodynamic Fluids
Previous: Linear Tearing Mode Theory
Richard Fitzpatrick
2016-01-23
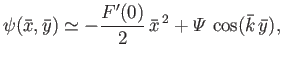
![]() and
and
![]() .
It follows that the normalized perturbed magnetic flux function,
.
It follows that the normalized perturbed magnetic flux function, ![]() ,
in the vicinity of the interface takes the form
,
in the vicinity of the interface takes the form
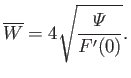
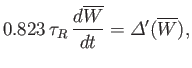
![$\displaystyle {\mit\Delta}'(\overline{W}) = \left[\frac{1}{\psi}\frac{d\psi}{d\bar{x}}\right]_{-\overline{W}/2}^{+\overline{W}/2}$](img2767.png)